题目内容
 在△ABC中,AB=AC,∠ACB=α,点M是BC的中点,点P是线段AM上的动点,将线段PC绕点P顺时针旋转2α得到线段PQ,线段BQ的延长线交AM延长线于点D.
在△ABC中,AB=AC,∠ACB=α,点M是BC的中点,点P是线段AM上的动点,将线段PC绕点P顺时针旋转2α得到线段PQ,线段BQ的延长线交AM延长线于点D.(1)如图1,若α=60°,点P与点M重合,则∠BDA=
(2)如图2,点P不与点A、点M重合,则∠BDA=
考点:旋转的性质
专题:
分析:(1)利用等腰三角形的性质得∠BMD=90°,结合条件可求得△BMQ是等边三角形,进一步可求得∠BDA;
(2)首先利用已知得出△CPD≌△BPD,进而得出∠PCD+∠PQD=∠PQB+∠PQD=180°,即可求出.
(2)首先利用已知得出△CPD≌△BPD,进而得出∠PCD+∠PQD=∠PQB+∠PQD=180°,即可求出.
解答:解:(1)∵AB=AC,M是BC的中点,
∴AM⊥BC,
∴∠BMD=90°,
∵∠CMQ=2α=120°,
∴∠BMP=60°,
∵BM=MC=MQ,
∴∠MBQ=60°,
∴∠BDA=90°-60°=30°,
故答案为:30°;
(2)如图,连接PB,CD,
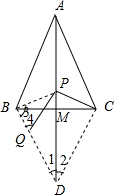
∵AC=AB,M是BC的中点,
∴AM⊥BC,
即AD为BC的垂直平分线,
∴BD=CD,BP=PC,PD=PD,
在△BPD与△CPD中,
,
∴△BPD≌△CPD(SSS),
∴∠CDA=∠BDA,∠PBD=∠PCD,
又∵PQ=PC,
∴PQ=PB,∠BDC=2∠1,∠4=∠PBQ=∠PCD,
∴∠PCD+∠PQD=∠4+∠PQD=180°,
∴∠CPQ+∠BDC=360°-(∠PCD+∠PQD)=180°,
∴∠BDA=180°-∠CPQ=180°-2α,
∴2∠BDA=180°-2α,
∴∠BDA=90°-α.
故答案为:90°-α.
∴AM⊥BC,
∴∠BMD=90°,
∵∠CMQ=2α=120°,
∴∠BMP=60°,
∵BM=MC=MQ,
∴∠MBQ=60°,
∴∠BDA=90°-60°=30°,
故答案为:30°;
(2)如图,连接PB,CD,

∵AC=AB,M是BC的中点,
∴AM⊥BC,
即AD为BC的垂直平分线,
∴BD=CD,BP=PC,PD=PD,
在△BPD与△CPD中,
|
∴△BPD≌△CPD(SSS),
∴∠CDA=∠BDA,∠PBD=∠PCD,
又∵PQ=PC,
∴PQ=PB,∠BDC=2∠1,∠4=∠PBQ=∠PCD,
∴∠PCD+∠PQD=∠4+∠PQD=180°,
∴∠CPQ+∠BDC=360°-(∠PCD+∠PQD)=180°,
∴∠BDA=180°-∠CPQ=180°-2α,
∴2∠BDA=180°-2α,
∴∠BDA=90°-α.
故答案为:90°-α.
点评:本题主要考查旋转的性质以及全等三角形的判定与性质,得出∠CPQ+∠BDC=360°-(∠PCD+∠PQD)=180°是解题关键.

练习册系列答案
相关题目
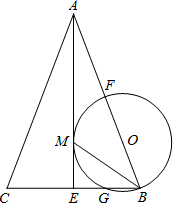 如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③a+b+c=0;④9a+3b+c<0,其中结论正确的是
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③a+b+c=0;④9a+3b+c<0,其中结论正确的是 如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D,C分别落在点F,E处,(点F,E都在AB所在的直线上),折痕为MN,则∠AMF等于
如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D,C分别落在点F,E处,(点F,E都在AB所在的直线上),折痕为MN,则∠AMF等于 老师布置了一道思考题:
老师布置了一道思考题: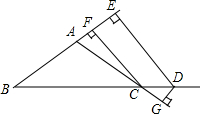 如图,已知AB=AC,DE⊥BA的延长线于E,DG⊥AC的延长线于点G,CF⊥BC于点F,试探索DE和CF+DG的关系.
如图,已知AB=AC,DE⊥BA的延长线于E,DG⊥AC的延长线于点G,CF⊥BC于点F,试探索DE和CF+DG的关系. 在平面直角坐标系中描出下列各点A(2,1),B(0,1),C(-2,3),D(4,3),并将各点用线段依次连接构成一个四边形ABCD.
在平面直角坐标系中描出下列各点A(2,1),B(0,1),C(-2,3),D(4,3),并将各点用线段依次连接构成一个四边形ABCD.