题目内容
 老师布置了一道思考题:
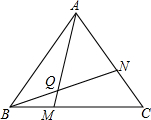
老师布置了一道思考题:如图,点M,N分别在等边三角形ABCD的BC、AC边上,且BM=CN,AM与BN交于点Q,求证:∠BQM=60°.
(1)请你完成这道思考题;
(2)做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?
②若将题中的M、N分别移动到BC、CA的延长线上,是否仍能得到∠BQM=60°?
…
请你作出判断,在下列横线上填“是”或“否”:①
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)易证△ABM≌△BCN,可得∠CBN=∠BAM,即可求得∠BQM=∠ABM=60°;
(2)①根据题干中给出条件可得∠CBN=∠BAM,即可证明△ABM≌△BCN,根据全等三角形对应边相等的性质即可解题;
②画出图形,易证CM=AN,和∠BAN=∠ACM=120°,即可证明△BAN≌△ACM,可得∠CAM=∠ABN,即可解题.
(2)①根据题干中给出条件可得∠CBN=∠BAM,即可证明△ABM≌△BCN,根据全等三角形对应边相等的性质即可解题;
②画出图形,易证CM=AN,和∠BAN=∠ACM=120°,即可证明△BAN≌△ACM,可得∠CAM=∠ABN,即可解题.
解答:证明:(1)∵在△ABM和△BCN中,
,
∴△ABM≌△BCN,(SAS)
∴∠CBN=∠BAM,
∵∠BAM+∠ABM+∠AMB=180°,∠CBN+∠AMB+∠BQM=180°,
∴∠BQM=∠ABM=60°;
(2)①∵∠BQM=∠ABM=60°,∠BAM+∠ABM+∠AMB=180°,∠CBN+∠AMB+∠BQM=180°,
∴∠CBN=∠BAM,
∵在△ABM和△BCN中,
,
∴△ABM≌△BCN,(ASA)
∴BM=CN,故答案为是;
②画出图形,
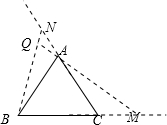
∵∠BAC=∠ACB=60°,
∴∠BAN=∠ACM=120°,
∵BM=CN,BC=AC
∴BM-BC=CN-AC,即CM=AN,
∵在△BAN和△ACM中,
,
∴△BAN≌△ACM,(SAS)
∴∠CAM=∠ABN,
∵∠ABN+∠ANB=60°,∠CAM=∠NAQ,
∴∠BQM=∠ANB+∠NAQ=60°.故答案为是.
|
∴△ABM≌△BCN,(SAS)
∴∠CBN=∠BAM,
∵∠BAM+∠ABM+∠AMB=180°,∠CBN+∠AMB+∠BQM=180°,
∴∠BQM=∠ABM=60°;
(2)①∵∠BQM=∠ABM=60°,∠BAM+∠ABM+∠AMB=180°,∠CBN+∠AMB+∠BQM=180°,
∴∠CBN=∠BAM,
∵在△ABM和△BCN中,
|
∴△ABM≌△BCN,(ASA)
∴BM=CN,故答案为是;
②画出图形,

∵∠BAC=∠ACB=60°,
∴∠BAN=∠ACM=120°,
∵BM=CN,BC=AC
∴BM-BC=CN-AC,即CM=AN,
∵在△BAN和△ACM中,
|
∴△BAN≌△ACM,(SAS)
∴∠CAM=∠ABN,
∵∠ABN+∠ANB=60°,∠CAM=∠NAQ,
∴∠BQM=∠ANB+∠NAQ=60°.故答案为是.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角、对应边相等的性质,本题中求证△BAN≌△ACM是解题的关键.

练习册系列答案
相关题目
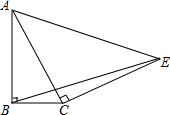 如图,在△ABC中,∠ABC=90°,过点C作AC的垂线CE,且CE=CA,连接AE、BE.
如图,在△ABC中,∠ABC=90°,过点C作AC的垂线CE,且CE=CA,连接AE、BE. 如图,将长方形ABCD沿AE折叠,使D点落在BC边上的点F处,已知AD=10,AB=8,求EC的长.
如图,将长方形ABCD沿AE折叠,使D点落在BC边上的点F处,已知AD=10,AB=8,求EC的长. 在△ABC中,AB=AC,∠ACB=α,点M是BC的中点,点P是线段AM上的动点,将线段PC绕点P顺时针旋转2α得到线段PQ,线段BQ的延长线交AM延长线于点D.
在△ABC中,AB=AC,∠ACB=α,点M是BC的中点,点P是线段AM上的动点,将线段PC绕点P顺时针旋转2α得到线段PQ,线段BQ的延长线交AM延长线于点D. 如图,在直角△ACB中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可由△ABC绕点C顺时针旋转得到,其中A′与A是对应点,点B′与B是对应点,点A、B、A′在同一条直线上,则A′B长为
如图,在直角△ACB中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可由△ABC绕点C顺时针旋转得到,其中A′与A是对应点,点B′与B是对应点,点A、B、A′在同一条直线上,则A′B长为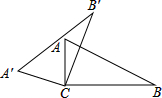 如图,将Rt△ABC绕C点逆时针旋转得到△A′B′C′,若∠A′BC=160°,则此图形旋转角是
如图,将Rt△ABC绕C点逆时针旋转得到△A′B′C′,若∠A′BC=160°,则此图形旋转角是 我们把两相邻边分别相等的四边形叫做“筝形”.如图,在筝形ABCD中,AB=AD,BC=DC,AC、BD相交于点O.
我们把两相邻边分别相等的四边形叫做“筝形”.如图,在筝形ABCD中,AB=AD,BC=DC,AC、BD相交于点O.