题目内容
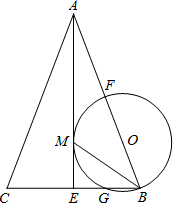 如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.(1)判断AE与⊙O的位置关系,并说明理由;
(2)当BC=4,AB=6时,求⊙O的半径.
考点:切线的判定
专题:
分析:(1)根据等腰三角形性质求出AE⊥BC,求出OM∥BC,推出AE⊥OM,根据切线的判定得出即可;
(2)证△AOM∽△ABE,得出比例式,代入求出即可.
(2)证△AOM∽△ABE,得出比例式,代入求出即可.
解答: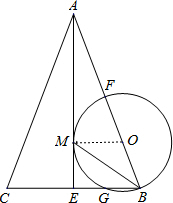 解:(1)AE与⊙O的位置关系是相切,
解:(1)AE与⊙O的位置关系是相切,
理由是:连接OM,
∵AB=AC,AE是角平分线,
∴AE⊥BC,
∵BM平分∠ABC,
∴∠ABM=∠EBM,
∵OM=OB,
∴∠ABM=∠OMB,
∴∠OMB=∠EBM,
∴OM∥BC,
∵AE⊥BC,
∴OM⊥AE,
∴AE是⊙O的切线;
(2)设⊙O的半径是R,
∵AB=AC,AE⊥BC,BC=4,
∴BE=CE=2,
∵OM∥BC,
∴△AOM∽△ABE,
∴
=
,
∴
=
,
解得:R=1.5,
即⊙O的半径是1.5.
 解:(1)AE与⊙O的位置关系是相切,
解:(1)AE与⊙O的位置关系是相切,理由是:连接OM,
∵AB=AC,AE是角平分线,
∴AE⊥BC,
∵BM平分∠ABC,
∴∠ABM=∠EBM,
∵OM=OB,
∴∠ABM=∠OMB,
∴∠OMB=∠EBM,
∴OM∥BC,
∵AE⊥BC,
∴OM⊥AE,
∴AE是⊙O的切线;
(2)设⊙O的半径是R,
∵AB=AC,AE⊥BC,BC=4,
∴BE=CE=2,
∵OM∥BC,
∴△AOM∽△ABE,
∴
| OM |
| BE |
| AO |
| AB |
∴
| R |
| 2 |
| 6-R |
| 6 |
解得:R=1.5,
即⊙O的半径是1.5.
点评:本题考查了平行线的性质和判定,切线的判定,等腰三角形的性质,相似三角形的性质和判定的应用,能综合运用性质进行推理是解此题的关键,题目比较好,有一定的难度.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 如图,将长方形ABCD沿AE折叠,使D点落在BC边上的点F处,已知AD=10,AB=8,求EC的长.
如图,将长方形ABCD沿AE折叠,使D点落在BC边上的点F处,已知AD=10,AB=8,求EC的长. 在△ABC中,AB=AC,∠ACB=α,点M是BC的中点,点P是线段AM上的动点,将线段PC绕点P顺时针旋转2α得到线段PQ,线段BQ的延长线交AM延长线于点D.
在△ABC中,AB=AC,∠ACB=α,点M是BC的中点,点P是线段AM上的动点,将线段PC绕点P顺时针旋转2α得到线段PQ,线段BQ的延长线交AM延长线于点D.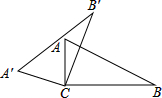 如图,将Rt△ABC绕C点逆时针旋转得到△A′B′C′,若∠A′BC=160°,则此图形旋转角是
如图,将Rt△ABC绕C点逆时针旋转得到△A′B′C′,若∠A′BC=160°,则此图形旋转角是 已知在△ABC中,D是AB上一点,P是AC上一点.
已知在△ABC中,D是AB上一点,P是AC上一点.