题目内容
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③a+b+c=0;④9a+3b+c<0,其中结论正确的是
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③a+b+c=0;④9a+3b+c<0,其中结论正确的是考点:二次函数图象与系数的关系
专题:
分析:根据图象与x轴的交点,可判断①,根据图象的开口方向、对称轴,可判断②,根据自变量的值得出相应的函数值,可判断③,根据函数的对称性,可判断④.
解答:解:①由图知:抛物线与x轴有两个不同的交点,则△=b2-4ac>0,∴b2>4ac,故①正确;
②抛物线开口向上,得:a>0;抛物线的对称轴为x=-
=1,b=-2a,故b<0;抛物线交y轴于负半轴,得:c<0;所以abc>0;故②正确;
③当x=1时,y=a+b+c<0,∴a+b+c=0错误,故③错误;
④根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称点是(3,0);
当x=-1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;故④正确;
所以这结论正确的有①②④.
故答案为:①②④.
②抛物线开口向上,得:a>0;抛物线的对称轴为x=-
| b |
| 2a |
③当x=1时,y=a+b+c<0,∴a+b+c=0错误,故③错误;
④根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称点是(3,0);
当x=-1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;故④正确;
所以这结论正确的有①②④.
故答案为:①②④.
点评:主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
 如图,将长方形ABCD沿AE折叠,使D点落在BC边上的点F处,已知AD=10,AB=8,求EC的长.
如图,将长方形ABCD沿AE折叠,使D点落在BC边上的点F处,已知AD=10,AB=8,求EC的长. 如图,已知△ABC和△BDE都为等腰直角三角形,点E在AB上,点F为CD的中点,连接BF.
如图,已知△ABC和△BDE都为等腰直角三角形,点E在AB上,点F为CD的中点,连接BF. 在△ABC中,AB=AC,∠ACB=α,点M是BC的中点,点P是线段AM上的动点,将线段PC绕点P顺时针旋转2α得到线段PQ,线段BQ的延长线交AM延长线于点D.
在△ABC中,AB=AC,∠ACB=α,点M是BC的中点,点P是线段AM上的动点,将线段PC绕点P顺时针旋转2α得到线段PQ,线段BQ的延长线交AM延长线于点D. 如图,在直角△ACB中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可由△ABC绕点C顺时针旋转得到,其中A′与A是对应点,点B′与B是对应点,点A、B、A′在同一条直线上,则A′B长为
如图,在直角△ACB中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可由△ABC绕点C顺时针旋转得到,其中A′与A是对应点,点B′与B是对应点,点A、B、A′在同一条直线上,则A′B长为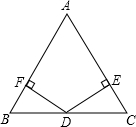 如图,在△ABC中,已知D是BC的中点,DF⊥AB于点F,DE⊥AC于点E,且DF=DE,那么AB=AC吗?你能用学过的知识完成这个问题吗?
如图,在△ABC中,已知D是BC的中点,DF⊥AB于点F,DE⊥AC于点E,且DF=DE,那么AB=AC吗?你能用学过的知识完成这个问题吗?