题目内容
 如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D,C分别落在点F,E处,(点F,E都在AB所在的直线上),折痕为MN,则∠AMF等于
如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D,C分别落在点F,E处,(点F,E都在AB所在的直线上),折痕为MN,则∠AMF等于考点:翻折变换(折叠问题)
专题:
分析:如图,根据题意结合图形得到∠D=∠MFE;证明∠A=∠MFA=70°,利用三角形的内角和定理即可解决问题.
解答: 解:由题意得:
解:由题意得:
∠D=∠MFE;
∵AB∥CD,
∴∠D+∠A=180°,而∠MFE+∠MFA=180°,
∴∠A=∠MFA=70°,
∴∠AMF=180°-2×70°=40°.
故该题答案为40°.
 解:由题意得:
解:由题意得:∠D=∠MFE;
∵AB∥CD,
∴∠D+∠A=180°,而∠MFE+∠MFA=180°,
∴∠A=∠MFA=70°,
∴∠AMF=180°-2×70°=40°.
故该题答案为40°.
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是根据翻折变换的性质找出图形中隐含的等量关系,灵活运用有关定理来分析、判断或解答.

练习册系列答案
相关题目
 在△ABC中,AB=AC,∠ACB=α,点M是BC的中点,点P是线段AM上的动点,将线段PC绕点P顺时针旋转2α得到线段PQ,线段BQ的延长线交AM延长线于点D.
在△ABC中,AB=AC,∠ACB=α,点M是BC的中点,点P是线段AM上的动点,将线段PC绕点P顺时针旋转2α得到线段PQ,线段BQ的延长线交AM延长线于点D.
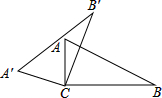 如图,将Rt△ABC绕C点逆时针旋转得到△A′B′C′,若∠A′BC=160°,则此图形旋转角是
如图,将Rt△ABC绕C点逆时针旋转得到△A′B′C′,若∠A′BC=160°,则此图形旋转角是 从△ABC的顶点A引三条线段:∠A的平分线AM,∠A的外角平分线AN,三角形外接圆的切线AK,点M、K、N依次排列在直线BC上,证明:MK=KN.
从△ABC的顶点A引三条线段:∠A的平分线AM,∠A的外角平分线AN,三角形外接圆的切线AK,点M、K、N依次排列在直线BC上,证明:MK=KN.