Question

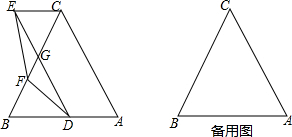
17．如图，在正方形ABCD中，AB=2$\sqrt{2}$，将∠BAD绕着点A顺时针旋转α（0＜α＜45），得到∠B′AD′，其中过点B作与对角线BD垂直的直线交射线AB′于点E，射线AD′与对角线BD交于点F，连接CF，并延长交AD于点M，当满足S_{四边形AEBF}=$\sqrt{2}$S_△CDM时，线段BE的长度为4$\sqrt{2}$-4．

Answer 1

分析 先根据旋转的性质得∠EAB=∠FAD=α，再根据正方形的性质得AB=AD，∠ADB=∠ABD=45°，则利用BE⊥BD得∠EBA=∠FDA=45°，于是可根据“ASA”判定△ABE≌△ADF，得到S_△ABE=S_△ADF，所以S_{四边形AEBF}=S_△ABD=4，则S_△CDM=2$\sqrt{2}$，利用三角形面积公式可计算出DM=2，过点F作FP⊥CD于点P，则FP∥DM，可得$\frac{FP}{MD}$=$\frac{CP}{CD}$，设FP=x，则PF=PD=x，代入即可求得x的值，在RtDPF中即可求得BE=DF=$\frac{PF}{cos∠DFP}$．

解答 解：∵∠BAD绕着点A顺时针旋转α°（0＜α＜45°），得到∠B′AD′，
∴∠EAB=∠FAD=α，
∵四边形ABCD为正方形，
∴AB=AD，∠ADB=∠ABD=45°，
∵BE⊥BD，
∴∠EBD=90°，
∴∠EBA=45°，
∴∠EBA=∠FDA，
在△ABE和△ADF中，
∵$\left\{\begin{array}{l}{∠EAB=∠FAD}\\{AB=AD}\\{∠EBA=∠FDA}\end{array}\right.$，
∴△ABE≌△ADF，
∴S_△ABE=S_△ADF，BE=DF，
∴S_{四边形AEBF}=S_△ABE+S_△ABF=S_△ADF+S_△ABF=S_△ABD=$\frac{1}{2}$×2$\sqrt{2}$×2$\sqrt{2}$=4，
∵S_{四边形AEBF}=$\sqrt{2}$S_△CDM，
∴S_△CDM=$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$，
∴$\frac{1}{2}$DM•2$\sqrt{2}$=2$\sqrt{2}$，解得DM=2，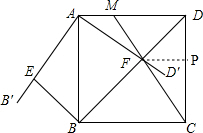

过点F作FP⊥CD于点P，则FP∥DM，
∴△CFP∽△CMD，
∴$\frac{FP}{MD}$=$\frac{CP}{CD}$，
设FP=x，
∵∠FDP=45°，
∴PF=PD=x，
则$\frac{x}{2}$=$\frac{2\sqrt{2}-x}{2\sqrt{2}}$，解得：x=4-2$\sqrt{2}$，
∴BE=DF=$\frac{PF}{cos∠DFP}$=$\frac{4-2\sqrt{2}}{\frac{\sqrt{2}}{2}}$=4$\sqrt{2}$-4，
故答案为：4$\sqrt{2}$-4．

点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了正方形的性质和全等三角形的判定与性质．