题目内容
5.如图1,在平面直角坐标系中,点A,B的坐标分别是(-2,0),(4,0),现同时将点A、B分别向上平移2个单位长度,再向右平移2个单位长度,得到A,B的对应点C,D.连接AC、BD、CD.
(1)点C的坐标为(0,2),点D的坐标为(6,2),四边形ABDC的面积为12.
(2)在x轴上是否存在一点E,使得△DEC的面积是△DEB面积的2倍?若存在,请求出点E的坐标;若不存在,请说明理由.
分析 (1)根据点平移的规律易得点C的坐标为(0,2),点D的坐标为(6,2);
(2)设点E的坐标为(x,0),根据△DEC的面积是△DEB面积的2倍和三角形面积公式得到$\frac{1}{2}$×6×2=2×$\frac{1}{2}$×|4-x|×2,解得x=1或x=7,然后写出点E的坐标.
解答 解:(1)∵点A,B的坐标分别是(-2,0),(4,0),现同时将点A、B分别向上平移2个单位长度,再向右平移2个单位长度得到A,B的对应点C,D,
∴点C的坐标为(0,2),点D的坐标为(6,2);
四边形ABDC的面积=2×(4+2)=12;
故答案为:(0,2),(6,2),12;
(2)存在.
设点E的坐标为(x,0),
∵△DEC的面积是△DEB面积的2倍,
∴$\frac{1}{2}$×6×2=2×$\frac{1}{2}$×|4-x|×2,解得x=1或x=7,
∴点E的坐标为(1,0)和(7,0).
点评 本题考查了坐标与图形性质:利用点的坐标得到线段的长和线段与坐标轴的关系.也考查了平行线的性质和分类讨论的思想.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
4. 如图,四边形ABCD是矩形,四边形AEFG是正方形,点E,G分别在AB,AD上,连接FC,过点E作EH∥FC交BC于点H.若∠BCF=30°,CD=4,CF=6,则正方形AEFG的面积为( )
如图,四边形ABCD是矩形,四边形AEFG是正方形,点E,G分别在AB,AD上,连接FC,过点E作EH∥FC交BC于点H.若∠BCF=30°,CD=4,CF=6,则正方形AEFG的面积为( )
 如图,四边形ABCD是矩形,四边形AEFG是正方形,点E,G分别在AB,AD上,连接FC,过点E作EH∥FC交BC于点H.若∠BCF=30°,CD=4,CF=6,则正方形AEFG的面积为( )
如图,四边形ABCD是矩形,四边形AEFG是正方形,点E,G分别在AB,AD上,连接FC,过点E作EH∥FC交BC于点H.若∠BCF=30°,CD=4,CF=6,则正方形AEFG的面积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5. 如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
 如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )| A. | (-1,0) | B. | (1,-2) | C. | (1,1) | D. | (0,-2) |
13. 如图,△ABC中,∠A=75°,∠B=50°,将△ABC绕点C按逆时针方向旋转,得到△A,B,C,点A的对应点A,落在AB边上,则∠BCA'的度数为( )
如图,△ABC中,∠A=75°,∠B=50°,将△ABC绕点C按逆时针方向旋转,得到△A,B,C,点A的对应点A,落在AB边上,则∠BCA'的度数为( )
 如图,△ABC中,∠A=75°,∠B=50°,将△ABC绕点C按逆时针方向旋转,得到△A,B,C,点A的对应点A,落在AB边上,则∠BCA'的度数为( )
如图,△ABC中,∠A=75°,∠B=50°,将△ABC绕点C按逆时针方向旋转,得到△A,B,C,点A的对应点A,落在AB边上,则∠BCA'的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
20. 下列四幅图案中,能通过平移如图所示的图案得到的是( )
下列四幅图案中,能通过平移如图所示的图案得到的是( )
 下列四幅图案中,能通过平移如图所示的图案得到的是( )
下列四幅图案中,能通过平移如图所示的图案得到的是( )| A. |  | B. |  | C. |  | D. |  |
14. 如图,△ABC绕点A逆时针旋转到△AB1C1,∠CAC1=75°,AB1∥BC1,则旋转角为( )
如图,△ABC绕点A逆时针旋转到△AB1C1,∠CAC1=75°,AB1∥BC1,则旋转角为( )
 如图,△ABC绕点A逆时针旋转到△AB1C1,∠CAC1=75°,AB1∥BC1,则旋转角为( )
如图,△ABC绕点A逆时针旋转到△AB1C1,∠CAC1=75°,AB1∥BC1,则旋转角为( )| A. | 120° | B. | 110° | C. | 100° | D. | 90° |
 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图.
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图. 如图,在正方形ABCD中,AB=2$\sqrt{2}$,将∠BAD绕着点A顺时针旋转α(0<α<45),得到∠B′AD′,其中过点B作与对角线BD垂直的直线交射线AB′于点E,射线AD′与对角线BD交于点F,连接CF,并延长交AD于点M,当满足S四边形AEBF=$\sqrt{2}$S△CDM时,线段BE的长度为4$\sqrt{2}$-4.
如图,在正方形ABCD中,AB=2$\sqrt{2}$,将∠BAD绕着点A顺时针旋转α(0<α<45),得到∠B′AD′,其中过点B作与对角线BD垂直的直线交射线AB′于点E,射线AD′与对角线BD交于点F,连接CF,并延长交AD于点M,当满足S四边形AEBF=$\sqrt{2}$S△CDM时,线段BE的长度为4$\sqrt{2}$-4.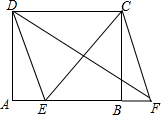 在矩形ABCD中,AD=3,AB=4,点E在线段AB上,将AE平移至BF.
在矩形ABCD中,AD=3,AB=4,点E在线段AB上,将AE平移至BF.