题目内容
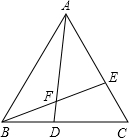 如图所示,△ABC是等边三角形,点D、E分别在BC、AC上,且CE=BD,BE、AD相交于点F.求证:
如图所示,△ABC是等边三角形,点D、E分别在BC、AC上,且CE=BD,BE、AD相交于点F.求证:(1)△ABD≌△BCE;
(2)△AEF∽△ABE.
考点:相似三角形的判定,全等三角形的判定,等边三角形的性质
专题:证明题
分析:(1)由△ABC是等边三角形,根据等边三角形的性质可得:AB=BC,∠ABD=∠C=60°,继而根据SAS即可证得△ABD≌△BCE;
(2)由△ABD≌△BCE,可证得∠BAD=∠CBE,进一步得到∠EAF=∠ABE,然后根据有两角对应相等的三角形相似,即可得△AEF∽△ABE.
(2)由△ABD≌△BCE,可证得∠BAD=∠CBE,进一步得到∠EAF=∠ABE,然后根据有两角对应相等的三角形相似,即可得△AEF∽△ABE.
解答:证明:(1)∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=∠BAC=60°,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(SAS);
(2)∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠EAF=∠ABE,
∵∠AEF=∠BEA,
∴△AEF∽△ABE.
∴AB=BC,∠ABD=∠C=∠BAC=60°,
在△ABD和△BCE中,
|
∴△ABD≌△BCE(SAS);
(2)∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠EAF=∠ABE,
∵∠AEF=∠BEA,
∴△AEF∽△ABE.
点评:此题考查了相似三角形的判定与性质与全等三角形的判定与性质.此题难度不大,解题的关键是注意数形结合思想的应用,注意有两角对应相等的三角形相似定理的应用.

练习册系列答案
相关题目
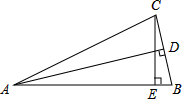 如图,AD、CE是△ABC的高,且AB=2BC.则AD与CE有怎样的数量关系?为什么?
如图,AD、CE是△ABC的高,且AB=2BC.则AD与CE有怎样的数量关系?为什么? 在△ABC中,∠A=60°,BD⊥AC,垂足为D,CE⊥AB,垂足为E,求证:△ADE∽△ABC.
在△ABC中,∠A=60°,BD⊥AC,垂足为D,CE⊥AB,垂足为E,求证:△ADE∽△ABC.