题目内容
如果直线y=-2x-1与直线y=3x+m相交于第三象限,则实数m的取值范围是 .
考点:两条直线相交或平行问题
专题:
分析:联立两直线解析式求出交点坐标,再根据交点在第三象限列出不等式组求解即可.
解答:解:联立
,
解得
,
∴交点坐标为(-
,
),
∵两直线相交于第三象限,
∴
,
解不等式①得,m>-1,
解不等式②得,m<
,
所以,不等式组的解集是-1<m<
,
即实数m的取值范围是:-1<m<
.
故答案为:-1<m<
.
|
解得
|
∴交点坐标为(-
| m+1 |
| 5 |
| 2m-3 |
| 5 |
∵两直线相交于第三象限,
∴
|
解不等式①得,m>-1,
解不等式②得,m<
| 3 |
| 2 |
所以,不等式组的解集是-1<m<
| 3 |
| 2 |
即实数m的取值范围是:-1<m<
| 3 |
| 2 |
故答案为:-1<m<
| 3 |
| 2 |
点评:本题考查了两直线相交的问题,点的坐标与解不等式组,求出用m表示的交点坐标并列出不等式组是解题的关键,也是本题的难点.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
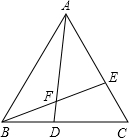 如图所示,△ABC是等边三角形,点D、E分别在BC、AC上,且CE=BD,BE、AD相交于点F.求证:
如图所示,△ABC是等边三角形,点D、E分别在BC、AC上,且CE=BD,BE、AD相交于点F.求证: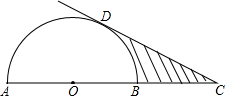 如图,AB是半圆O的直径,延长OB至点C,使BC=AO,过点C作半圆的切线,切点为D.如果半圆的半径为r,图中阴影部分的面积为S,则S可用r表示为
如图,AB是半圆O的直径,延长OB至点C,使BC=AO,过点C作半圆的切线,切点为D.如果半圆的半径为r,图中阴影部分的面积为S,则S可用r表示为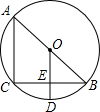 如图,AB是⊙O的直径,BC是弦,OD⊥BC,垂足为E,交⊙O于D,连接AC.
如图,AB是⊙O的直径,BC是弦,OD⊥BC,垂足为E,交⊙O于D,连接AC.