题目内容
已知对于任意实数x,二次函数y1=kx2-x+1的值恒为正;而对于一次函数y2=kx+b,当自变量的取值范围为-3≤x≤6,相应函数的取值范围是-5≤y≤-2;则函数y=y1+y2的解析式为 .
考点:抛物线与x轴的交点,一次函数的性质
专题:计算题
分析:对于任意实数x,二次函数y1=kx2-x+1的值恒为正,得到二次函数开口向上且与x轴没有交点,求出k的范围,利用k的范围及一次函数性质得到一次函数为增函数,确定出一次函数图象上两点,代入一次函数求出k与b的值,即可确定出y.
解答:解:对于任意实数x,二次函数y1=kx2-x+1的值恒为正,
得到k>0,△=1-4k<0,即k>
,
对于一次函数y2=kx+b,当自变量的取值范围为-3≤x≤6,相应函数的取值范围是-5≤y≤-2,
得到一次函数为增函数,即x=-3时,y=-5;x=6时,y=-2,
代入得:
,
解得:k=
,b=-4,
则y=y1+y2=
x2-x+1+
x-4=
x2-
x-3.
故答案为:
x2-
x-3
得到k>0,△=1-4k<0,即k>
| 1 |
| 4 |
对于一次函数y2=kx+b,当自变量的取值范围为-3≤x≤6,相应函数的取值范围是-5≤y≤-2,
得到一次函数为增函数,即x=-3时,y=-5;x=6时,y=-2,
代入得:
|
解得:k=
| 1 |
| 3 |
则y=y1+y2=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
故答案为:
| 1 |
| 3 |
| 2 |
| 3 |
点评:此题考查了抛物线与x轴交点,以及一次函数性质,弄清题意是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
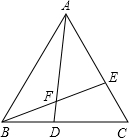 如图所示,△ABC是等边三角形,点D、E分别在BC、AC上,且CE=BD,BE、AD相交于点F.求证:
如图所示,△ABC是等边三角形,点D、E分别在BC、AC上,且CE=BD,BE、AD相交于点F.求证: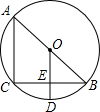 如图,AB是⊙O的直径,BC是弦,OD⊥BC,垂足为E,交⊙O于D,连接AC.
如图,AB是⊙O的直径,BC是弦,OD⊥BC,垂足为E,交⊙O于D,连接AC.