题目内容
在△ABC中，∠A=60°，BD⊥AC，垂足为D，CE⊥AB，垂足为E，求证：△ADE∽△ABC．考点：相似三角形的判定
专题：证明题
分析：由BD⊥AC，CE⊥AB得到∠AEC=∠ADB=90°，利用∠EAC=∠DAB可判断△AEC∽△ADB，则
=
，利用比例性质得
=
，加上∠EAD=∠CAB，根据三角形相似的判定方法即可得到结论．
| AE |
| AD |
| AC |
| AB |
| AE |
| AC |
| AD |
| AB |
解答：证明：∵BD⊥AC，CE⊥AB，
∴∠AEC=∠ADB=90°，
而∠EAC=∠DAB，
∴△AEC∽△ADB，
∴
=
，
∴
=
，
∵∠EAD=∠CAB，
∴△ADE∽△ABC．
∴∠AEC=∠ADB=90°，
而∠EAC=∠DAB，
∴△AEC∽△ADB，
∴
| AE |
| AD |
| AC |
| AB |
∴
| AE |
| AC |
| AD |
| AB |
∵∠EAD=∠CAB，
∴△ADE∽△ABC．
点评：本题考查了相似三角形的判定与性质：有两组角对应相等的两三角形相似；有两组对应边的比相等且夹角相等的两个三角形相似；相似三角形的对应边的比相等．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
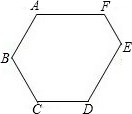如图，在六边形ABCDEF中，AF∥CD，AB∥ED，∠A=140°，∠B=100°，∠E=90°．求∠C、∠D、∠F的度数．
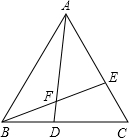如图所示，△ABC是等边三角形，点D、E分别在BC、AC上，且CE=BD，BE、AD相交于点F．求证：