题目内容
1.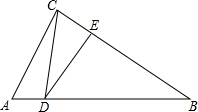 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=4,点D在AB边上,点E在BC边上,且∠CDE=30°,AD=1,则BE的长=$\frac{35\sqrt{3}}{12}$.
如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=4,点D在AB边上,点E在BC边上,且∠CDE=30°,AD=1,则BE的长=$\frac{35\sqrt{3}}{12}$.
分析 根据题意可得出AB=8,BC=4$\sqrt{3}$,BD=AB-AD=7,设BE=x,则CE=4$\sqrt{3}$-x,然后判断△CDE∽△CBD,继而利用相似三角形的性质可得关于x的方程,解方程求出x的值即可.
解答 解:∵在Rt△ABC中,∠ACB=90°,∠A=60°,
∴∠B=30°
∵AC=4,
∴AB=8,
∴BC=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,BD=AB-AD=7,
在△ACD中,利用余弦定理可得CD2=AC2+AD2-2AC•ADcos∠A=16+1-4=13,
∴CD=$\sqrt{13}$,
又∵∠CDE=∠CBD=30°,∠ECD=∠DCB(同一个角),
∴△CDE∽△CBD,
∴$\frac{CE}{CD}=\frac{CD}{CB}$,
设BE=x,则CE=4$\sqrt{3}$-x,
即$\frac{4\sqrt{3}-x}{\sqrt{13}}=\frac{\sqrt{13}}{4\sqrt{3}}$,
解得:x=$\frac{35\sqrt{3}}{12}$,
∵BE=$\frac{35\sqrt{3}}{12}$,
故答案为:$\frac{35\sqrt{3}}{12}$.
点评 此题考查了相似三角形的判定和性质以及含30度角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半.解答本题的关键是判断出△CDE∽△CBD,利用余弦定理得出CD的长.

练习册系列答案
相关题目
9.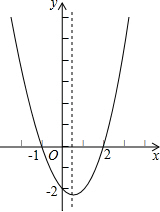 如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )
如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )
 如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )
如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )| A. | a>0,b<0,c>0 | B. | b2-4ac<0 | ||
| C. | 当-1<x<2时,y>0 | D. | 当x<$\frac{1}{2}$时,y随x的增大而减小 |
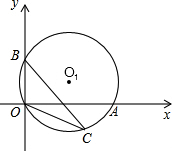 如图,在平面直角坐标系中,过点O的⊙O1与两坐标轴分别交于A、B两点A(4,0),B(0,2),点C在弧OA上,则tan∠BCO为$\frac{1}{2}$.
如图,在平面直角坐标系中,过点O的⊙O1与两坐标轴分别交于A、B两点A(4,0),B(0,2),点C在弧OA上,则tan∠BCO为$\frac{1}{2}$.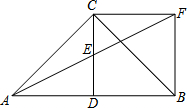 如图,在△ABC中,AC=BC,AC⊥BC,D是AB的中点,E是CD的中点,过点C作CF∥AB交AE的延长线于点F,连结BF.试判断四边形BDCF的形状,并证明你的结论.
如图,在△ABC中,AC=BC,AC⊥BC,D是AB的中点,E是CD的中点,过点C作CF∥AB交AE的延长线于点F,连结BF.试判断四边形BDCF的形状,并证明你的结论.