题目内容
13.解下列方程:(1)x2+4x+1=0
(2)$\frac{6}{x-2}$=$\frac{x}{x+3}$-1.
分析 (1)(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方;
(2)把分式方程去分母化为整式方程,根据配方法解答即可.
解答 解:(1)x2+4x+4=3,
(x+2)2=3,
x=-2±$\sqrt{3}$,
x1=-2+$\sqrt{3}$,x2=-2-$\sqrt{3}$;
(2)方程两边同时乘(x-2)(x+3),
6(x+3)=x(x-2)-(x-2)(x+3)
x=-$\frac{4}{3}$,
当x=-$\frac{4}{3}$时,(x-2)(x+3)≠0,
∴原方程的解为:x=-$\frac{4}{3}$.
点评 本题考查的是配方法解一元二次方程,掌握形如x2+px+q=0型:第一步移项,把常数项移到右边;第二步配方,左右两边加上一次项系数一半的平方;第三步左边写成完全平方式;第四步,直接开方是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.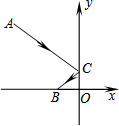 如图,一束光线从点A(-3,3)出发,经过y轴上的点C反射后经过点B(-1,0),则光线从点A到点B经过的路线长是( )
如图,一束光线从点A(-3,3)出发,经过y轴上的点C反射后经过点B(-1,0),则光线从点A到点B经过的路线长是( )
 如图,一束光线从点A(-3,3)出发,经过y轴上的点C反射后经过点B(-1,0),则光线从点A到点B经过的路线长是( )
如图,一束光线从点A(-3,3)出发,经过y轴上的点C反射后经过点B(-1,0),则光线从点A到点B经过的路线长是( )| A. | 3 | B. | $\frac{7}{2}$ | C. | 5 | D. | 6 |
2.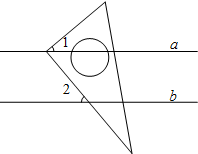 如图,a∥b,将-块三角板的直角顶点放在直线a上,若∠1=42°,则∠2的度数为( )
如图,a∥b,将-块三角板的直角顶点放在直线a上,若∠1=42°,则∠2的度数为( )
 如图,a∥b,将-块三角板的直角顶点放在直线a上,若∠1=42°,则∠2的度数为( )
如图,a∥b,将-块三角板的直角顶点放在直线a上,若∠1=42°,则∠2的度数为( )| A. | 46° | B. | 48° | C. | 56° | D. | 72° |
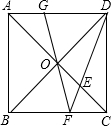 如图,O为正方形ABCD对角线的交点,E是线段OC的中点,DE的延长线交BC边于点F,连接并延长FO交AD于点G.若AB=2,则GF=$\frac{2\sqrt{10}}{3}$.
如图,O为正方形ABCD对角线的交点,E是线段OC的中点,DE的延长线交BC边于点F,连接并延长FO交AD于点G.若AB=2,则GF=$\frac{2\sqrt{10}}{3}$.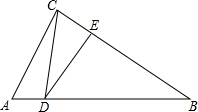 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=4,点D在AB边上,点E在BC边上,且∠CDE=30°,AD=1,则BE的长=$\frac{35\sqrt{3}}{12}$.
如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=4,点D在AB边上,点E在BC边上,且∠CDE=30°,AD=1,则BE的长=$\frac{35\sqrt{3}}{12}$.