题目内容
12.某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不能超过10000元,且生产B产品要超过38件,问有哪几种符合条件的生产方案?
(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,才能使生产这批产品的成本最低?请直接写出方案.
分析 (1)设甲种材料每千克x元,乙种材料每千克y元,根据题意列出方程,解方程即可;
(2)设生产B产品a件,生产A产品(60-a)件.根据题意得出一元一次不等式组,解不等式组即可得出结果;
(3)设生产成本为W元,根据题意得出W是a的一次函数,即可得出结果.
解答 解:(1)设甲种材料每千克x元,乙种材料每千克y元,
依题意得:$\left\{\begin{array}{l}{x+y=60}\\{2x+3y=155}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=25}\\{y=35}\end{array}\right.$;
答:甲种材料每千克25元,乙种材料每千克35元.
(2)设生产B产品a件,生产A产品(60-a)件.
依题意得:$\left\{\begin{array}{l}{(25×4+35×1)(60-x)+(35×3+25×3)a≤10000}&{\;}\\{a>38}&{\;}\end{array}\right.$,
解得:38<a≤$\frac{380}{9}$;
∵a的值为非负整数,
∴a=39、40、41、42;
答:共有如下四种方案:
| A(件) | 21 | 20 | 19 | 18 |
| B(件) | 39 | 40 | 41 | 42 |
设生产成本为W元,则W与a的关系式为:
W=(25×4+35×1+40)(60-a)+(35×3+25×3+50)a=55a+10 500,
即W是a的一次函数,
∵k=55>0
∴W随a增大而增大
∴当a=39时,总成本最低;
即生产A产品21件,B产品39件成本最低.
点评 本题考查了二元一次方程组的应用、一元一次不等式组的应用、一次函数的应用;根据题意中的数量关系列出方程组、不等式组、一次函数关系式是解决问题的关键.

练习册系列答案
相关题目
7.将一张面值50元的人民币,兑换成5元或10元的零钱,那么兑换方案共有( )
| A. | 5种 | B. | 6种 | C. | 7种 | D. | 8种 |
17.同时抛掷两枚质地均匀的正方体,正方体的六个面上分别刻有1到6的整数,下列事件是不可能事件的是( )
| A. | 点数之和为13 | B. | 点数之和小于3 | ||
| C. | 点数之和大于4且小于8 | D. | 点数之和为12 |
2.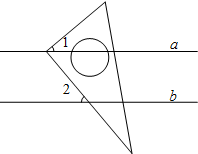 如图,a∥b,将-块三角板的直角顶点放在直线a上,若∠1=42°,则∠2的度数为( )
如图,a∥b,将-块三角板的直角顶点放在直线a上,若∠1=42°,则∠2的度数为( )
 如图,a∥b,将-块三角板的直角顶点放在直线a上,若∠1=42°,则∠2的度数为( )
如图,a∥b,将-块三角板的直角顶点放在直线a上,若∠1=42°,则∠2的度数为( )| A. | 46° | B. | 48° | C. | 56° | D. | 72° |
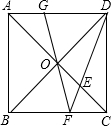 如图,O为正方形ABCD对角线的交点,E是线段OC的中点,DE的延长线交BC边于点F,连接并延长FO交AD于点G.若AB=2,则GF=$\frac{2\sqrt{10}}{3}$.
如图,O为正方形ABCD对角线的交点,E是线段OC的中点,DE的延长线交BC边于点F,连接并延长FO交AD于点G.若AB=2,则GF=$\frac{2\sqrt{10}}{3}$.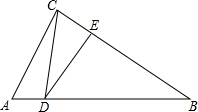 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=4,点D在AB边上,点E在BC边上,且∠CDE=30°,AD=1,则BE的长=$\frac{35\sqrt{3}}{12}$.
如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=4,点D在AB边上,点E在BC边上,且∠CDE=30°,AD=1,则BE的长=$\frac{35\sqrt{3}}{12}$.