题目内容
16. 如图,在矩形ABCD中,AB=3,AD=4,若以点A为圆心,以4为半径作⊙A,则点A,点B,点C,点D四点中在⊙A外的是C.
如图,在矩形ABCD中,AB=3,AD=4,若以点A为圆心,以4为半径作⊙A,则点A,点B,点C,点D四点中在⊙A外的是C.
分析 要确定点与圆的位置关系,主要确定点与圆心的距离与半径的大小关系;本题可由勾股定理等性质算出点与圆心的距离d,则d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
解答 解:∵CA=$\sqrt{{3}^{2}+{4}^{2}}$=5>4,
∴点,C在⊙A外,
∵AD═4,
∴点D在⊙A上外;
AB=3<4,
∴点B在⊙A内,
故答案为:C.
点评 本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列说法正确的是( )
| A. | 点(2,4)在函数y=2x+4的图象上 | |
| B. | 已知甲,乙两组数据的个数相同且平均数相等,若甲组数据的方差S甲2=0.06,乙组数据的方差S乙2=0.105,则甲的波动比乙的波动小 | |
| C. | Rt△ABC的边a=3、b=4,则第三边c=5 | |
| D. | 二元一次方程组$\left\{\begin{array}{l}{x+y=3}\\{2x-3y=1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ |
4.正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A,B,C,D把原正方形分割成一些三角形(互相不重叠):

(1)填写表:
(2)若用y表示内部有n个点时正方形ABCD被分割成的三角形的个数,试写出y=2(n+1)(用含有n的代数式表示,n是正整数);
(3)正方形ABCD能否被分割成2016个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.

(1)填写表:
| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … |
| 分割成的三角形的个数 | 4 | 6 | 8 | 10 | … |
(3)正方形ABCD能否被分割成2016个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
6.根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2015年5月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见表:
若2015年5月份,该市居民甲用电100度,交电费60元.
(1)上表中,a=0.6;若居民乙用电200度,则应交电费122.5元;
(2)若某用户某月用电量超过300度,设用电量为x度,请你用含x的代数式表示应交的电费;
(3)试行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价为每度0.62元?
| 一户居民一个月用电量的范围 | 电费价格(单位:元/度) |
| 不超过150度 | a |
| 超过150度但不超过300度的部分 | 0.65 |
| 超过300度的部分 | 0.9 |
(1)上表中,a=0.6;若居民乙用电200度,则应交电费122.5元;
(2)若某用户某月用电量超过300度,设用电量为x度,请你用含x的代数式表示应交的电费;
(3)试行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价为每度0.62元?
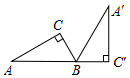 如图,Rt△A'BC'是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C'在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,则Rt△ABC旋转到Rt△A'BC'所扫过的面积为$\frac{16}{3}$π+2$\sqrt{3}$.
如图,Rt△A'BC'是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C'在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,则Rt△ABC旋转到Rt△A'BC'所扫过的面积为$\frac{16}{3}$π+2$\sqrt{3}$. 已知一次函数y=ax+b(a≠0)的图象经过A(3,0),B(0,3)两点.
已知一次函数y=ax+b(a≠0)的图象经过A(3,0),B(0,3)两点.