题目内容
1．在Rt△ABC中，∠ACB=90°，AC=3，tanB=$\frac{4}{3}$，求AB的值．分析 利用锐角三角函数定义求出BC的长，再利用勾股定理求出AB的长即可．
解答 
解：在Rt△ABC中，∠ACB=90°，AC=3，tanB=$\frac{4}{3}$，
∵tanB=$\frac{AC}{BC}$，
∴BC=$\frac{AC}{tanB}$=$\frac{3}{\frac{4}{3}}$=$\frac{9}{4}$，
则AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\frac{15}{4}$．
点评 此题考查了锐角三角函数定义，熟练掌握锐角三角函数定义是解本题的关键．
练习册系列答案
天天向上口算本系列答案
相关题目
16．下列式子中，能与2a合并的是（ ）
| A． | 2a3 | B． | -3a+b | C． | -10a | D． | -a2b |
如图，AO=BO=2，∠AOB=90°，△A′、C、D分别与点A重合，在边BO上、在边BO的延长线上，且A′C=A′D=$\sqrt{5}$，将△A′CD沿射线OB平移，设平移距离为x（其中0＜x＜3），平移后的图形与△ABO重叠部分的面积为S．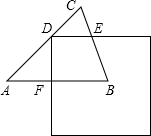
如图，在△ABC中，AB=AC=1，∠A=60°，边长为1的正方形的一个顶点D在边AC上，与△ABC另两边分别交于点E、F，DE∥AB，将正方形平移，使点D保持在AC上（D不与A重合），设AF=x，正方形与△ABC重叠部分的面积为y．
如图，在矩形ABCD中，AB=3，AD=4，若以点A为圆心，以4为半径作⊙A，则点A，点B，点C，点D四点中在⊙A外的是C．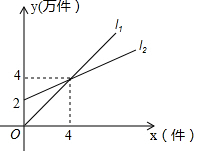
如图，l1表示某产品一天的销售收入与销售量的关系；l2表示该产品一天的销售成本与销售量的关系．则销售收入y1与销售量之间的函数关系式y1=x，销售成本y2与销售量之间的函数关系式y2=$\frac{1}{2}$x+2，当一天的销售量超过x＞4时，生产该产品才能获利．（提示：利润=收入-成本）
11．已知$\frac{1}{x}$-$\frac{1}{y}$=5，则分式$\frac{2x+3xy-2y}{x-2xy-y}$的值为（ ）
| A． | 1 | B． | 5 | C． | $\frac{13}{7}$ | D． | $\frac{13}{3}$ |