题目内容
8.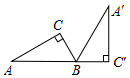 如图,Rt△A'BC'是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C'在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,则Rt△ABC旋转到Rt△A'BC'所扫过的面积为$\frac{16}{3}$π+2$\sqrt{3}$.
如图,Rt△A'BC'是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C'在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,则Rt△ABC旋转到Rt△A'BC'所扫过的面积为$\frac{16}{3}$π+2$\sqrt{3}$.
分析 先利用勾股定理计算出AC=2$\sqrt{3}$,再利用三角函数得到∠ABC=60°,接着根据旋转的性质得到∠A′B′C′=∠ABC=60°,△ABC≌△A′B′C′,所以∠ABA′=120°,
然后根据扇形面积公式,利用Rt△ABC旋转到Rt△A'BC'所扫过的面积=S扇形ABA′+S△A′B′C′进行计算即可.
解答 解:∵∠C=90°,BC=2,AB=4,
∴AC=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵tan∠ABC=$\frac{AC}{BC}$=$\sqrt{3}$,
∴∠ABC=60°,
∵Rt△A'BC'是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C'在同一条直线上,
∴∠A′B′C′=∠ABC=60°,△ABC≌△A′B′C′,
∴∠ABA′=120°,
∴Rt△ABC旋转到Rt△A'BC'所扫过的面积=S扇形ABA′+S△A′B′C′
=$\frac{120•π•{4}^{2}}{360}$+$\frac{1}{2}$×2×2$\sqrt{3}$
=$\frac{16}{3}$π+2$\sqrt{3}$.
故答案为$\frac{16}{3}$π+2$\sqrt{3}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
相关题目
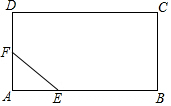 如图,有一块矩形钢板ABCD,先截去了一个直角三角形AEF,得到一个五边形EBCDF,已知AB=200cm,BC=160cm,AE=60cm,AF=40cm,要从这块钢板上再截出一块矩形板料,如何设计才能使矩形板料的面积最大?最大面积是多少?
如图,有一块矩形钢板ABCD,先截去了一个直角三角形AEF,得到一个五边形EBCDF,已知AB=200cm,BC=160cm,AE=60cm,AF=40cm,要从这块钢板上再截出一块矩形板料,如何设计才能使矩形板料的面积最大?最大面积是多少? 如图,在矩形ABCD中,AB=3,AD=4,若以点A为圆心,以4为半径作⊙A,则点A,点B,点C,点D四点中在⊙A外的是C.
如图,在矩形ABCD中,AB=3,AD=4,若以点A为圆心,以4为半径作⊙A,则点A,点B,点C,点D四点中在⊙A外的是C.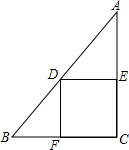 如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y. 如图是每个面上都有一个汉字的正方体的表面展开图,那么在原正方体的表面上与汉字“爱”相对的面上的汉字是丽.
如图是每个面上都有一个汉字的正方体的表面展开图,那么在原正方体的表面上与汉字“爱”相对的面上的汉字是丽.