题目内容
19.AC为⊙O的直径,B是⊙O外一点,AB交⊙O于E点,过E点作⊙O的切线,交BC于D点,DE=DC,作EF⊥AC于F点,交AD于M点.(1)求证:BC是⊙O的切线;
(2)求证:EM=FM.
分析 (1)连接CE,根据等腰三角形的性质得到∠1=∠2,由弦切角定理得到∠2=∠BAC,根据圆周角定理得到∠AEC=90°,于是得到∠BAC+∠3=90°,等量代换得到∠1+∠3=90°,求得∠ACB=90°,即可得到结论;
(2)由BC⊥AC,EF⊥AC求得EF∥BC,于是得到△AEM∽△ABD,△ANF∽△ACD,根据相似三角形的性质得到$\frac{EM}{BD}=\frac{AM}{AD}$,$\frac{MF}{CD}=\frac{AM}{AD}$,等量代换得到$\frac{EM}{BD}=\frac{FM}{CD}$,根据比例的性质即可得到结论.
解答 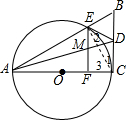 解:(1)连接CE,
解:(1)连接CE,
∵DE=CD,
∴∠1=∠2,
∵DE是⊙O的切线,
∴∠2=∠BAC,
∵AC为⊙O的直径,
∴∠AEC=90°,
∴∠BAC+∠3=90°,
∴∠1+∠3=90°,
∴∠ACB=90°,
∴BC是⊙O的切线;
(2)∵∠1+∠3=90°,
∴BC⊥AC,
∵EF⊥AC,
∴EF∥BC,
∴△AEM∽△ABD,△ANF∽△ACD,
∴$\frac{EM}{BD}=\frac{AM}{AD}$,$\frac{MF}{CD}=\frac{AM}{AD}$,
∴$\frac{EM}{BD}=\frac{FM}{CD}$,
∵∠1=∠2,
∴∠1+∠B=∠2+∠BED=90°,
∴∠B=∠BED,
∴DE=BD,
∴BD=CD,
∴EM=FM.
点评 本题考查了切线的判定和性质,相似三角形的判定和性质,正确的画出图形是解题的关键.

练习册系列答案
相关题目
11.对于抛物线y=ax2-4ax+3a下列说法:①对称轴为x=2;②抛物线与x轴两交点的坐标分别为(1,0),(3,0);③顶点坐标为(2,-a);④若a<0,当x>2时,函数y随x的增大而增大,其中正确的结论有( )个.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.-$\frac{1}{6}$的相反数是( )
| A. | -6 | B. | -$\frac{1}{6}$ | C. | $\frac{1}{6}$ | D. | 6 |
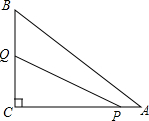 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P从点A出发,沿AC以每秒1个单位的速度向终点C运动,点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动,当点P停止运动时,点Q也随之停止,点P,Q同时出发,设点P的运动时间为t(秒).
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P从点A出发,沿AC以每秒1个单位的速度向终点C运动,点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动,当点P停止运动时,点Q也随之停止,点P,Q同时出发,设点P的运动时间为t(秒). 如图,△ABC中,∠ACB=90°,CD是高,若∠A=30°,BD=1,则BC=2,AD=3.
如图,△ABC中,∠ACB=90°,CD是高,若∠A=30°,BD=1,则BC=2,AD=3.