题目内容
17.⊙O是△ABC的外接圆,⊙O的半径R=2,AD⊥BC,且$\frac{AD}{AB}$=$\frac{\sqrt{7}}{3}$,求弦AC的长.分析 作直径AE,连接BE,则AE=2R=4,由圆周角定理得出∠ABE=90°,∠E=∠C,证出△ACD∽△AEB,得出对应边成比例,即可求出弦AC的长.
解答 解:作直径AE,连接BE,如图所示: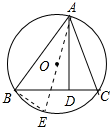
则AE=2R=4,∠ABE=90°,∠E=∠C,
∵AD⊥BC,
∴∠ADC=90°=∠ABE,
∴△ACD∽△AEB,
∴$\frac{AC}{AE}=\frac{AD}{AB}$,
即$\frac{AC}{4}=\frac{\sqrt{7}}{3}$,
解得:AC=$\frac{4\sqrt{7}}{3}$.
点评 本题考查了三角形的外接圆、圆周角定理、相似三角形的判定与性质;熟练掌握圆周角定理,通过作辅助线证明三角形相似是解决问题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
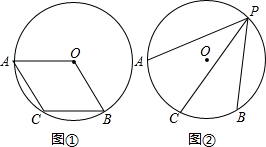 已知,A、B是⊙O上两点,∠AOB=120°,C为AB的中点.
已知,A、B是⊙O上两点,∠AOB=120°,C为AB的中点.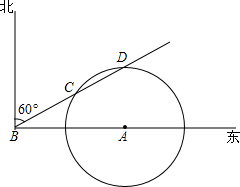 如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.
如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.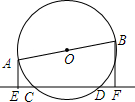 圆O的直径AB=10cm,CD长是圆O的$\frac{1}{6}$,AE⊥CD于E,BF⊥CD于F.
圆O的直径AB=10cm,CD长是圆O的$\frac{1}{6}$,AE⊥CD于E,BF⊥CD于F.