题目内容
8. 如图,△ABC中,∠ACB=90°,CD是高,若∠A=30°,BD=1,则BC=2,AD=3.
如图,△ABC中,∠ACB=90°,CD是高,若∠A=30°,BD=1,则BC=2,AD=3.
分析 根据三角形内角和定理求出∠B=60°,∠BCD=30°,根据含30°角的直角三角形性质求出BC,再求出AB,即可得出答案.
解答 解:∵在△ACB中,∠ACB=90°,∠A=30°,
∴∠B=60°,
∵CD是高,
∴∠CDB=90°,
∴∠BCD=30°,
∵BD=1,
∴BC=2BD=2,
∴AB=2BC=4,
%AD=4-1=3.
故答案为:2,3.
点评 本题考查了三角形内角和定理和含30°角的直角三角形性质的应用,能根据含30°角的直角三角形性质得出BC=2BD和AB=2BC是解此题的关键.

练习册系列答案
相关题目
3.抛物线y=-2x2+1的对称轴是( )
| A. | 直线x=$\frac{1}{2}$ | B. | y轴 | C. | 直线x=2 | D. | 直线x=-$\frac{1}{2}$ |
13. 如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为3,则周长是( )
如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为3,则周长是( )
 如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为3,则周长是( )
如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为3,则周长是( )| A. | 2m+6 | B. | 4m+12 | C. | 2m+3 | D. | m+6 |

 如图是一数值转换机,若输出的结果为-50,则输入的x的值为±5.
如图是一数值转换机,若输出的结果为-50,则输入的x的值为±5.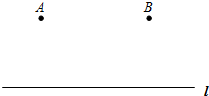 如图:A村和B村在公路l同侧,且AB=3千米,两村距离公路都是2千米.现决定在公路l上建立一个供水站P,要求使PA+PB最短.
如图:A村和B村在公路l同侧,且AB=3千米,两村距离公路都是2千米.现决定在公路l上建立一个供水站P,要求使PA+PB最短.