题目内容
14.将两个斜边长相等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②,连接D1B,则∠E1D1B的度数为15°.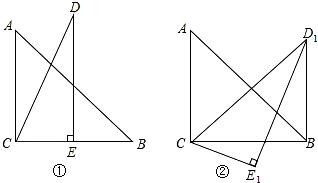
分析 根据直角三角形两锐角互余求出∠DCE=60°,旋转的性质可得∠BCE1=15°,然后求出∠BCD1=45°,从而得到∠BCD1=∠A,利用“边角边”证明△ABC和△D1CB全等,根据全等三角形对应角相等可得∠BD1C=∠ABC=45°,再根据∠E1D1B=∠BD1C-∠CD1E1计算即可得解.
解答 解:∵∠CED=90°,∠D=30°,
∴∠DCE=60°,
∵△DCE绕点C顺时针旋转15°,
∴∠BCE1=15°,
∴∠BCD1=60°-15°=45°,
∴∠BCD1=∠A,
在△ABC和△D1CB中,
$\left\{\begin{array}{l}{AC=CB}&{\;}\\{∠BC{D}_{1}=∠A}&{\;}\\{AB=C{D}_{1}}&{\;}\end{array}\right.$,
∴△ABC≌△D1CB(SAS),
∴∠BD1C=∠ABC=45°,
∴∠E1D1B=∠BD1C-∠CD1E1=45°-30°=15°.
故答案为:15°.
点评 本题考查了旋转的性质,等腰直角三角形的性质,全等三角形的判定与性质,熟记性质并求出△ABC和△D1CB全等是解题的关键.

练习册系列答案
相关题目
17. 如图是一个零件的立体图,该零件的俯视图是( )
如图是一个零件的立体图,该零件的俯视图是( )
 如图是一个零件的立体图,该零件的俯视图是( )
如图是一个零件的立体图,该零件的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
 (1)计算:|-2|-$\sqrt{9}$+(-$\frac{1}{2}$)-1;
(1)计算:|-2|-$\sqrt{9}$+(-$\frac{1}{2}$)-1; 如图所示,把长方形纸片ABCD折叠,使CD落在EF处,折痕为GH,在这个图形中,有没有关于某条直线成轴对称的两个图形呢?如果有,你能据此得到一些相等的线段和一些相等的角吗?
如图所示,把长方形纸片ABCD折叠,使CD落在EF处,折痕为GH,在这个图形中,有没有关于某条直线成轴对称的两个图形呢?如果有,你能据此得到一些相等的线段和一些相等的角吗? 如图,在△ABC中,AB=AC,∠B=70°,将△ABC绕点C顺时针旋转α(其中0°<α<70°)后得到△A′B′C,连接AA′,则∠AA′B′=50°-$\frac{1}{2}$α(用含α的式子表示).
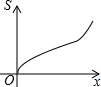
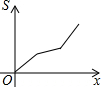
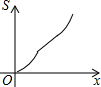
如图,在△ABC中,AB=AC,∠B=70°,将△ABC绕点C顺时针旋转α(其中0°<α<70°)后得到△A′B′C,连接AA′,则∠AA′B′=50°-$\frac{1}{2}$α(用含α的式子表示).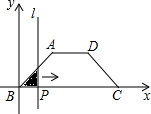 如图,在四边形ABCD中,AD∥BC,AB=DC,以点B为原点,BC边所在的直线为x轴建立平面直角坐标系,直线l与y轴重合且向右平移,若其扫过的面积(阴影部分)为S,设向右平移的距离BP为x,则S关于x的函数图象大致是( )
如图,在四边形ABCD中,AD∥BC,AB=DC,以点B为原点,BC边所在的直线为x轴建立平面直角坐标系,直线l与y轴重合且向右平移,若其扫过的面积(阴影部分)为S,设向右平移的距离BP为x,则S关于x的函数图象大致是( )