题目内容
10.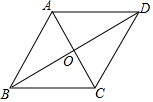 如图,在?ABCD中,对角线AC,BD交于点O,AB=10,AO=6,BO=8,则下列结论中,错误的是( )
如图,在?ABCD中,对角线AC,BD交于点O,AB=10,AO=6,BO=8,则下列结论中,错误的是( )| A. | AC⊥BD | B. | 四边形ABCD是菱形 | ||
| C. | AC=BD | D. | △ABO≌△CDO |
分析 根据勾股定理的逆定理可得?ABCD的对角线互相垂直,根据对角线互相垂直的平行四边形是菱形可得?ABCD是菱形,由菱形ABCD中,对角线AC、BD交于点O,根据菱形的两条对角线互相垂直且平分,由SAS可证△ABO≌△CDO;即可求得答案.
解答 解:∵AB=10,AO=6,BO=8,
AB2=AO2+BO2,
∴∠AOB=90°,
∴AC⊥BD,故A正确,不符合题意;
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形,故B正确,不符合题意;
菱形的对角线不一定相等,故C错误,符合题意;
∵四边形ABCD是菱形,
∴AC=CO,BO=DO,
在△ABO≌△CDO中,
$\left\{\begin{array}{l}{AC=CO}\\{∠AOB=∠COD}\\{BO=DO}\end{array}\right.$,
∴△ABO≌△CDO,故D正确,不符合题意.
故选C.
点评 此题考查了菱形的判定与性质.此题比较简单,注意熟记性质定理是关键,注意数形结合思想的应用.

练习册系列答案
相关题目
20.要使式子$\sqrt{x+2}$有意义,则x的取值范围是( )
| A. | x>0 | B. | x≥-2 | C. | x≥2 | D. | x≤2 |
 已知在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,4),B(1,1),C(3,2).
已知在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,4),B(1,1),C(3,2).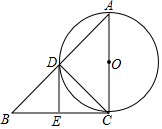 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.