题目内容
15．在△ABC中，∠C=90°，若斜边AB=4，则AB2+BC2+AC2=32．分析 根据在△ABC中，∠C=90°，斜边AB=4可得出BC2+AC2=AB2=16，据此可得出结论．
解答 解：∵在△ABC中，∠C=90°，斜边AB=4，
∴BC2+AC2=AB2=16，
∴AB2+BC2+AC2=16+16=32．
故答案为：32．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
5．下列说法正确的是（ ）
| A． | 0没有平方根 | B． | -1的平方根是-1 | ||
| C． | 4的算术平方根是2 | D． | （-3）2的平方根是3 |
10．
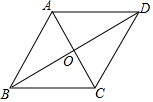如图，在?ABCD中，对角线AC，BD交于点O，AB=10，AO=6，BO=8，则下列结论中，错误的是（ ）
如图，在?ABCD中，对角线AC，BD交于点O，AB=10，AO=6，BO=8，则下列结论中，错误的是（ ）| A． | AC⊥BD | B． | 四边形ABCD是菱形 | ||
| C． | AC=BD | D． | △ABO≌△CDO |
20．下列运算中，正确的是（ ）
| A． | $\sqrt{9}$=±3 | B． | $\root{3}{-8}$=2 | C． | ±$\sqrt{9}$=3 | D． | ${（\root{3}{-8}）}^{2}$=4 |
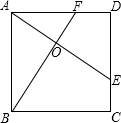如图，E，F分别是正方形ABCD的边CD，AD上的点，且CE=DF，AE，BF相交于点O，下列结论：①AE=BF；②AE⊥BF；③AO=OE；④∠CEA=∠DFB；⑤S△AOB=S四边形DEOF中正确的有（ ）