题目内容
5.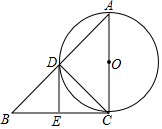 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.(1)求证:点E是边BC的中点;
(2)当AC=BC时,一点O、D、E、C为顶点的四边形是什么特殊四边形?试说明你的结论.
分析 (1)连接OD,如图,先判断BC为⊙O的切线,再利用切线长定理得到ED=EC,则∠1=∠2,接着证明∠3=∠B得到ED=EB,从而得到EB=EC;
(2)当AC=BC时,利用DE=CE=$\frac{1}{2}$BC,OC=$\frac{1}{2}$AC得到OD=OC=CE=DE,加上∠OCE=90°,于是可判定四边形OCED为正方形.
解答 (1)证明:连接OD,如图,
∵∠ACB=90°,
∴BC为⊙O的切线,
∵DE为切线,
∴ED=EC,
∴∠1=∠2,
∵AC为直径,
∴∠ADC=90°,
∴∠2+∠3=90°,∠B+∠1=90°,
∴∠3=∠B,
∴ED=EB,
∴EB=EC,
即点E是边BC的中点;
(2)解:当AC=BC时,
DE=CE=$\frac{1}{2}$BC,
而OC=$\frac{1}{2}$AC,
∴OD=OC=CE=DE,
而∠OCE=90°,
∴四边形OCED为正方形.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径;灵活应用切线长定理.也考查了正方形的判定.

练习册系列答案
相关题目
15.顺次连接任意四边形ABCD各边的中点所得四边形是( )
| A. | 一定是平行四边形 | B. | 一定是菱形 | ||
| C. | 一定是矩形 | D. | 一定是正方形 |
20.计算(am)3•an的结果是( )
| A. | a | B. | a3m+n | C. | C、a3(m+n) | D. | a5mn |
10.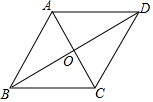 如图,在?ABCD中,对角线AC,BD交于点O,AB=10,AO=6,BO=8,则下列结论中,错误的是( )
如图,在?ABCD中,对角线AC,BD交于点O,AB=10,AO=6,BO=8,则下列结论中,错误的是( )
 如图,在?ABCD中,对角线AC,BD交于点O,AB=10,AO=6,BO=8,则下列结论中,错误的是( )
如图,在?ABCD中,对角线AC,BD交于点O,AB=10,AO=6,BO=8,则下列结论中,错误的是( )| A. | AC⊥BD | B. | 四边形ABCD是菱形 | ||
| C. | AC=BD | D. | △ABO≌△CDO |
15.已知x=1是关于x的方程2x-a=1的解,则a的值是( )
| A. | 1 | B. | -1 | C. | -3 | D. | 3 |
 如图,在△ABC,AB=AC,点D为BC的中点,AE是∠BAC外角的平分线,DE∥AB交AE于E,则四边形ADCE的形状是矩形.
如图,在△ABC,AB=AC,点D为BC的中点,AE是∠BAC外角的平分线,DE∥AB交AE于E,则四边形ADCE的形状是矩形.