题目内容
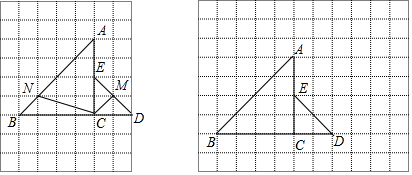
19.在每个小正方形的边长为1的网格中,等腰直角三角形ACB与ECD的顶点都在网格点上,点N、M分别为线段AB、DE上的动点,且BN=EM.(Ⅰ)如图①,当BN=$\sqrt{2}$时,计算CN+CM的值等于$\sqrt{10}$+$\sqrt{2}$;
(Ⅱ)当CN+CM取得最小值时,请在如图②所示的网格中,用无刻度的直尺,画出线段CN和CM,并简要说明点M和点N的位置是如何找到的(不要求证明).
分析 (1)根据当BN=EM=$\sqrt{2}$时,点N和点M在格点上,运用勾股定理进行计算即可得到CN+CM的值;
(2)取格点P、Q,使得PB=CE,PB⊥BC,QE=CB,QE⊥AC,连接CP交AB于N,连接CQ交DE于M,则根据全等三角形的对应边相等,以及两点之间线段最短,可得线段CN和CM即为所求.
解答 解:(1)当BN=EM=$\sqrt{2}$时,点N和点M在格点上,
∴CN+CM=$\sqrt{{3}^{2}+{1}^{2}}$+$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{10}$+$\sqrt{2}$;
(2)如图所示,取格点P、Q,使得PB=CE,PB⊥BC,QE=CB,QE⊥AC,
连接CP交AB于N,连接CQ交DE于M,则线段CN和CM即为所求.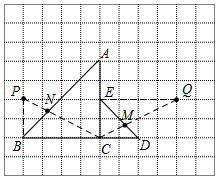
理由如下:根据等腰直角三角形ACB与ECD的顶点都在网格点上,可得∠PBN=∠CEM=45°,∠CBN=∠QEM=45°,而BN=EM,
故△BPN≌△ECM,△CBN≌△QEM,
∴PN=CM,CN=QM,
∴当P,N,C三点共线时,CM+CN=PN+CN=PC(最短),
当Q,M,C三点共线时,CM+CN=CM+MQ=QC(最短),
∴点M和点N的位置符合题意.
点评 本题主要考查了复杂作图,勾股定理以及全等三角形判定与性质的综合应用,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
相关题目
10.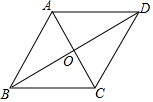 如图,在?ABCD中,对角线AC,BD交于点O,AB=10,AO=6,BO=8,则下列结论中,错误的是( )
如图,在?ABCD中,对角线AC,BD交于点O,AB=10,AO=6,BO=8,则下列结论中,错误的是( )
 如图,在?ABCD中,对角线AC,BD交于点O,AB=10,AO=6,BO=8,则下列结论中,错误的是( )
如图,在?ABCD中,对角线AC,BD交于点O,AB=10,AO=6,BO=8,则下列结论中,错误的是( )| A. | AC⊥BD | B. | 四边形ABCD是菱形 | ||
| C. | AC=BD | D. | △ABO≌△CDO |
7.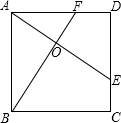 如图,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④∠CEA=∠DFB;⑤S△AOB=S四边形DEOF中正确的有( )
如图,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④∠CEA=∠DFB;⑤S△AOB=S四边形DEOF中正确的有( )
 如图,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④∠CEA=∠DFB;⑤S△AOB=S四边形DEOF中正确的有( )
如图,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④∠CEA=∠DFB;⑤S△AOB=S四边形DEOF中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
11.根据如图所示的统计表可知:a=5,b=20.
| 等级 | 频数 | 频率 |
| 一等奖 | a | 0.1 |
| 二等奖 | 10 | 0.2 |
| 三等奖 | b | 0.4 |
| 优秀奖 | 15 | 0.3 |
 如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接AF交对角线于点E,连接EC
如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接AF交对角线于点E,连接EC