题目内容
7.先化简,再求值:$\frac{a-3}{2a-4}$÷(a+2-$\frac{5}{a-2}$),其中a=$\sqrt{3}$-3.分析 先将$\frac{a-3}{2a-4}$÷(a+2-$\frac{5}{a-2}$)进行化简,然后将a=$\sqrt{3}$-3代入求解即可.
解答 解:原式=$\frac{a-3}{2(a-2)}$÷[$\frac{{a}^{2}-4}{a-2}$-$\frac{5}{a-2}$]
=$\frac{a-3}{2(a-2)}$÷$\frac{{a}^{2}-9}{a-2}$
=$\frac{a-3}{2(a-2)}$×$\frac{a-2}{(a+3)(a-3)}$
=$\frac{1}{2(a+3)}$.
当a=$\sqrt{3}$-3时,
原式=$\frac{1}{2\sqrt{3}}$=$\frac{\sqrt{3}}{6}$.
点评 本题考查了分式的化简求值,解答本题的关键在于先将$\frac{a-3}{2a-4}$÷(a+2-$\frac{5}{a-2}$)进行化简,然后将a=$\sqrt{3}$-3代入求解.

练习册系列答案
相关题目
18.将一副三角板按如图①的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,得到如图②,测得CG=6$\sqrt{2}$,则AC长是( )
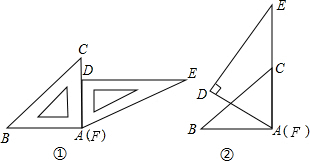

| A. | 6+2$\sqrt{3}$ | B. | 9 | C. | 10 | D. | 6+6$\sqrt{2}$ |
2.某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,设每次降价的百分率为x,则下面所列的方程中正确的是( )
| A. | 560(1-x)2=315 | B. | 560(1+x)2=315 | C. | 560(1-2x)2=315 | D. | 560(1-x2)=315 |
16. 如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )
如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )
 如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )
如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:3 |
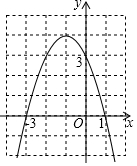 二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么一元二次方程ax2+bx+c=m(a≠0,m为常数且m≤4)的两根之和为( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么一元二次方程ax2+bx+c=m(a≠0,m为常数且m≤4)的两根之和为( ) 如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD、OD.
如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD、OD.