题目内容
15.已知线段AB=20cm,直线AB上有一点C,且BC=8cm,M是线段BC的中点,则AM的长是24或16cm.分析 根据题意,分两种情况:(1)点B在点A、C的中间时;(2)点C在点A、B的中间时;求出AM的长是多少即可.
解答 解:(1)如图1,点B在点A、C的中间时, ,
,
∵M是线段BC的中点,
∴BM=8÷2=4(cm),
∴AM=AB+BM=20+4=24(cm).
(2)如图2,点C在点A、B的中间时, ,
,
∵M是线段BC的中点,
∴BM=8÷2=4(cm),
∴AM=AB-BM=20-4=16(cm).
故答案为:24或16.
点评 此题主要考查了两点间的距离的含义和求法,考查了分类讨论思想的应用,要熟练掌握,解答此题的关键是要明确:线段的中点将线段分成长度相等的两个线段.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
3. 如图,O是线段AB的中点,C在线段OB上,AC=6,CB=3,则OC的长等于( )
如图,O是线段AB的中点,C在线段OB上,AC=6,CB=3,则OC的长等于( )
 如图,O是线段AB的中点,C在线段OB上,AC=6,CB=3,则OC的长等于( )
如图,O是线段AB的中点,C在线段OB上,AC=6,CB=3,则OC的长等于( )| A. | 0.5 | B. | 1 | C. | 1.5 | D. | 2 |
10.如图,将左边正方形剪成四块,恰能拼成右边的矩形,若a=2,则b的值是( )
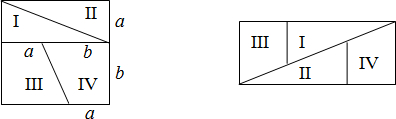

| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$+1 | D. | $\sqrt{3}$+1 |
20.使式子$\frac{\sqrt{2-x}}{x}$有意义的实数x的取值范围是( )
| A. | x≤2 | B. | x<2且x≠0 | C. | x≤2且x≠0 | D. | x<2 |
4.如果∠1的补角是∠2,且∠1>∠2,那么∠2是( )
| A. | 直角 | B. | 锐角 | C. | 钝角 | D. | 平角 |
 如图,已知△ABC,∠ABC,∠ACB的角平分线交于点O,连接AO并延长交BC于D,OH⊥BC于H,若∠BAC=60°,OH=3cm,OA长为( )cm.
如图,已知△ABC,∠ABC,∠ACB的角平分线交于点O,连接AO并延长交BC于D,OH⊥BC于H,若∠BAC=60°,OH=3cm,OA长为( )cm.