题目内容
 如图,在梯形ABCD中,AB∥DC;
如图,在梯形ABCD中,AB∥DC;(1)已知∠A=∠B,求证:AD=BC;
(2)已知AD=BC,求证:∠A=∠B.
考点:梯形
专题:证明题
分析:(1)过C作CE∥AD,可证明四边形ADCE是平行四边形,根据平行四边形的性质可得AD=CE,根据AD∥CE,可得∠A=∠CEB,根据等量代换可得∠CEB=∠B,进而得到CE=BC,从而可得AD=BC;
(2)过C作CE∥AD,可证明四边形ADCE是平行四边形,根据平行四边形的性质可得AD=CE,再由条件AD=BC可得CE=BC,根据等边对等角可得∠B=∠CEB,再根据平行线的性质可得∠A=∠CEB,利用等量代换可得∠B=∠A.
(2)过C作CE∥AD,可证明四边形ADCE是平行四边形,根据平行四边形的性质可得AD=CE,再由条件AD=BC可得CE=BC,根据等边对等角可得∠B=∠CEB,再根据平行线的性质可得∠A=∠CEB,利用等量代换可得∠B=∠A.
解答:证明:(1)过C作CE∥AD,
∵AB∥DC,
∴四边形ADCE是平行四边形,
∴AD=CE,
∵AD∥CE,
∴∠A=∠CEB,
∵∠A=∠B,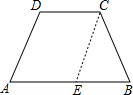
∴∠CEB=∠B,
∴CE=CB,
∴AD=CB;
(2)过C作CE∥AD,
∵AB∥DC,
∴四边形ADCE是平行四边形,
∴AD=CE,
∵AD=BC,
∴CE=CB,
∴∠B=∠CEB,
∵AD∥CE,
∴∠A=∠CEB,
∴∠B=∠A.
∵AB∥DC,
∴四边形ADCE是平行四边形,
∴AD=CE,
∵AD∥CE,
∴∠A=∠CEB,
∵∠A=∠B,

∴∠CEB=∠B,
∴CE=CB,
∴AD=CB;
(2)过C作CE∥AD,
∵AB∥DC,
∴四边形ADCE是平行四边形,
∴AD=CE,
∵AD=BC,
∴CE=CB,
∴∠B=∠CEB,
∵AD∥CE,
∴∠A=∠CEB,
∴∠B=∠A.
点评:此题主要考查了梯形,关键是正确做出平行线,构造平行四边形,再结合平行四边形的性质进行证明.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
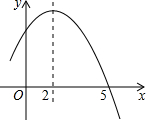 如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是( )
如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是( )| A、-1<x<5 |
| B、x>5 |
| C、x<-1且x>5 |
| D、x<-1或x>5 |
 如图,AD=BD=CD,∠CBD=20°,则∠BAC=( )
如图,AD=BD=CD,∠CBD=20°,则∠BAC=( )| A、40° | B、60° |
| C、70° | D、80° |
 如图,在△ABC中,∠ACB=2∠B,∠ACB的平分线交AB于D,DE⊥BC,垂足为E,请写出一对全等三角形,并说明理由.
如图,在△ABC中,∠ACB=2∠B,∠ACB的平分线交AB于D,DE⊥BC,垂足为E,请写出一对全等三角形,并说明理由.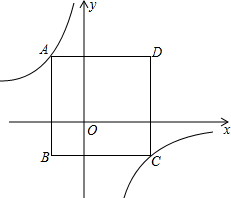 如图,边长为6的正方形ABCD置于平面直角坐标系xOy中,且AB平行于y轴,已知点A的横坐标为-2,反比例函数y=
如图,边长为6的正方形ABCD置于平面直角坐标系xOy中,且AB平行于y轴,已知点A的横坐标为-2,反比例函数y= 如图,在△ABC的顶点A的直线上取两点D、E,连接BD、CE,已知∠1=∠2,∠3=∠4,∠5=∠6;求证:BD∥AC.
如图,在△ABC的顶点A的直线上取两点D、E,连接BD、CE,已知∠1=∠2,∠3=∠4,∠5=∠6;求证:BD∥AC.