题目内容
在△ABC中,若∠C=
∠B=
∠A,则△ABC是 三角形(按角分类)
| 1 |
| 2 |
| 1 |
| 3 |
考点:三角形内角和定理
专题:
分析:设∠C=x°,由∠C=
∠B=
∠A,可得:∠B=2∠C=2x,∠A=3∠C=3x,然后由三角形内角和定理即可求出∠A、∠B、∠C的度数,即可判断三角形的形状.
| 1 |
| 2 |
| 1 |
| 3 |
解答:解:∠C=x°,
∵∠C=
∠B=
∠A,
∴∠B=2∠C=2x,∠A=3∠C=3x,
∵∠A+∠B+∠C=180°,
即:3x+2x+x=180°,
解得:x=30°,
∴∠C=30°,∠A=3∠C=90°,∠B=2∠C=60°,
∴此三角形是直角三角形.
故答案为:直角.
∵∠C=
| 1 |
| 2 |
| 1 |
| 3 |
∴∠B=2∠C=2x,∠A=3∠C=3x,
∵∠A+∠B+∠C=180°,
即:3x+2x+x=180°,
解得:x=30°,
∴∠C=30°,∠A=3∠C=90°,∠B=2∠C=60°,
∴此三角形是直角三角形.
故答案为:直角.
点评:此题考查了三角形内角和定理及直角三角形的判定,解题的关键是:由∠C=
∠B=
∠A,得到:∠B=2∠C,∠A=3∠C.
| 1 |
| 2 |
| 1 |
| 3 |

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 小明设计了某个产品的包装盒,由于粗心,少设计了其中一部分,请你把它补上,使其成为一个两面均有盖的正方体盒子,共有
小明设计了某个产品的包装盒,由于粗心,少设计了其中一部分,请你把它补上,使其成为一个两面均有盖的正方体盒子,共有 如图,在梯形ABCD中,AB∥DC;
如图,在梯形ABCD中,AB∥DC;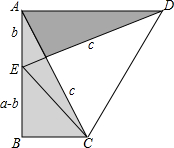 如图,两个全等的直角△ABC和△DAE,两直角边的长分别为a,b,斜边长为c,使用两种不同的方法表示梯形ABCD的面积,并以此来验证勾股定理.
如图,两个全等的直角△ABC和△DAE,两直角边的长分别为a,b,斜边长为c,使用两种不同的方法表示梯形ABCD的面积,并以此来验证勾股定理.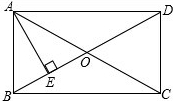 如图,在矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD于E,若BE:ED=1:3,AD=6.
如图,在矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD于E,若BE:ED=1:3,AD=6. 某人A地出发,先去小河l边饮马,然后B地办事,欲使所走路程最短,求饮马的位置应选在何处,说明理由.
某人A地出发,先去小河l边饮马,然后B地办事,欲使所走路程最短,求饮马的位置应选在何处,说明理由.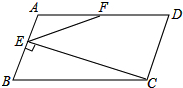 如图,?ABCD中,BC=2CD,CE⊥AB于点E,F为AD的中点,若∠EFD=k∠AEF,求k的值.
如图,?ABCD中,BC=2CD,CE⊥AB于点E,F为AD的中点,若∠EFD=k∠AEF,求k的值.