题目内容
 如图,在△ABC中,∠ACB=2∠B,∠ACB的平分线交AB于D,DE⊥BC,垂足为E,请写出一对全等三角形,并说明理由.
如图,在△ABC中,∠ACB=2∠B,∠ACB的平分线交AB于D,DE⊥BC,垂足为E,请写出一对全等三角形,并说明理由.考点:全等三角形的判定
专题:
分析:可以得到△BDE≌△CDE,根据CD平分∠ACB,得∠DCE=
∠ACB,再由∠ACB=2∠B,即可得出∠DCE=∠B根据全等三角形的判定方法AAS即可得出△BDE≌△CDE.
| 1 |
| 2 |
解答:解:以△BDE≌△CDE为例.
理由如下:
∵CD平分∠ACB,
∴∠DCE=
∠ACB,
∵∠ACB=2∠B,
∴∠B=
∠ACB,
∴∠DCE=∠B,
∵DE⊥BC,
∴∠DEC=∠DEB=90°
在△BDE和△CDE中,
,
∴△BDE≌△CDE(AAS).
理由如下:
∵CD平分∠ACB,
∴∠DCE=
| 1 |
| 2 |
∵∠ACB=2∠B,
∴∠B=
| 1 |
| 2 |
∴∠DCE=∠B,
∵DE⊥BC,
∴∠DEC=∠DEB=90°
在△BDE和△CDE中,
|
∴△BDE≌△CDE(AAS).
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 如图,在以BD为直径的⊙O上,
如图,在以BD为直径的⊙O上, |
| AB |
 |
| BC |
| A、70° | B、30° |
| C、35° | D、40° |
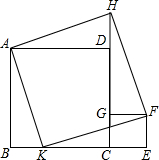 已知,如图,四边形ABCD和CEFG都是正方形,点K在BC上,延长CD到点H,使DH=CE=BK.求证:四边形AKFH是正方形.
已知,如图,四边形ABCD和CEFG都是正方形,点K在BC上,延长CD到点H,使DH=CE=BK.求证:四边形AKFH是正方形. 如图,在梯形ABCD中,AB∥DC;
如图,在梯形ABCD中,AB∥DC;