题目内容
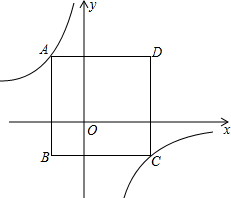 如图,边长为6的正方形ABCD置于平面直角坐标系xOy中,且AB平行于y轴,已知点A的横坐标为-2,反比例函数y=
如图,边长为6的正方形ABCD置于平面直角坐标系xOy中,且AB平行于y轴,已知点A的横坐标为-2,反比例函数y=| k |
| x |
考点:反比例函数图象上点的坐标特征
专题:计算题
分析:先根据正方形的性质确定A点坐标,再根据反比例函数图象上点的坐标特征确定反比例函数解析式,然后根据反比例函数的性质求解.
解答:解:∵点A的横坐标为-2,正方形ABCD的边长为6,
∴点C的横坐标为4,
∵AB平行于y轴,
∴点A与点C关于直线y=x对称,
∴A(-2,4),C(4,-2),
∴k=-2×4=-8,
∴反比例函数解析式为y=-
,
当-2≤y≤4时,则x≥4或x≤-2.
故答案为x≥4或x≤-2.
∴点C的横坐标为4,
∵AB平行于y轴,
∴点A与点C关于直线y=x对称,
∴A(-2,4),C(4,-2),
∴k=-2×4=-8,
∴反比例函数解析式为y=-
| 8 |
| x |
当-2≤y≤4时,则x≥4或x≤-2.
故答案为x≥4或x≤-2.
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
| k |
| x |

练习册系列答案
相关题目
下列说法正确的是( )
| A、相等的角是对顶角 |
| B、一对同旁内角的平分线互相垂直 |
| C、对顶角的平分线在一条直线上 |
| D、同位角相等 |
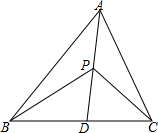 如图,△ABC中,AB>AC,AD是∠A的平分线,点P是线段AD上的任意一点,则AB+PC与AC+PB的大小关系是( )
如图,△ABC中,AB>AC,AD是∠A的平分线,点P是线段AD上的任意一点,则AB+PC与AC+PB的大小关系是( )| A、AB+PC>AC+PB |
| B、AB+PC<AC+PB |
| C、AB+PC=AC+PB |
| D、不确定 |
 如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=10,试求△PMN的周长.
如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=10,试求△PMN的周长.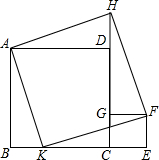 已知,如图,四边形ABCD和CEFG都是正方形,点K在BC上,延长CD到点H,使DH=CE=BK.求证:四边形AKFH是正方形.
已知,如图,四边形ABCD和CEFG都是正方形,点K在BC上,延长CD到点H,使DH=CE=BK.求证:四边形AKFH是正方形. 如图,在梯形ABCD中,AB∥CD,AD=DC=BD=a,BC=b,求AC的长.
如图,在梯形ABCD中,AB∥CD,AD=DC=BD=a,BC=b,求AC的长. 如图,在梯形ABCD中,AB∥DC;
如图,在梯形ABCD中,AB∥DC; 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C的面积和是10,则正方形D的边长为
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C的面积和是10,则正方形D的边长为