题目内容
19.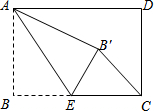 如图,长方形的宽AB=3,长BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.
如图,长方形的宽AB=3,长BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.(1)线段AB′的长为3;
(2)当△CEB′为直角三角形时,CE的长为1或$\frac{5}{2}$.
分析 (1)由折叠的性质可得:AB′=AB=3;
(2)当△CEB′为直角三角形,可知有两种情况:①当∠CB′E=90°时与②当∠B′EC=90°时;然后分别求解即可求得答案.
解答 解:(1)由折叠的性质可得:AB′=AB=3;
故答案为:3;
(2)当△CEB′为直角三角形时,有两种情况:
①当∠CB′E=90°时,如答图1所示.
则A,B′,C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
在Rt△ABC中,AB=3,BC=4,
∴AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴EB=EB′,AB=AB′=3,
∴CB′=5-3=2,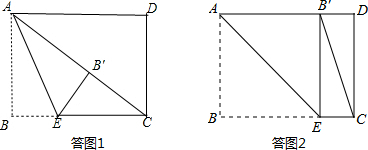 设BE=x,则EB′=x,CE=4-x,
设BE=x,则EB′=x,CE=4-x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2,
∴x2+22=(4-x)2,解得x=$\frac{3}{2}$,
∴BE=$\frac{3}{2}$,
∴CE=BC-BE=$\frac{5}{2}$;
②当∠B′EC=90°时,如答图2所示.
此时ABEB′为正方形,
∴BE=AB=3,
∴CE=BC-BE=4-3=1;
综上所述,CE的长为1或$\frac{5}{2}$.
故答案为:1或$\frac{5}{2}$.
点评 本题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了矩形的性质以及勾股定理.注意本题有两种情况,需要分类讨论,避免漏解.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
14.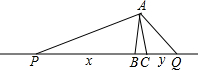 如图,在△ABC中,AB=AC,∠BAC=20°,P,Q在直线BC上,且∠PAQ=100°.设BP=x,CQ=y,则下列结论正确的是( )
如图,在△ABC中,AB=AC,∠BAC=20°,P,Q在直线BC上,且∠PAQ=100°.设BP=x,CQ=y,则下列结论正确的是( )
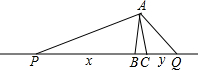 如图,在△ABC中,AB=AC,∠BAC=20°,P,Q在直线BC上,且∠PAQ=100°.设BP=x,CQ=y,则下列结论正确的是( )
如图,在△ABC中,AB=AC,∠BAC=20°,P,Q在直线BC上,且∠PAQ=100°.设BP=x,CQ=y,则下列结论正确的是( )| A. | 当x≠y时,△APB≌△AQC | B. | 当x=y时,∠APB=∠PAB=45° | ||
| C. | 当x=2y时,$\frac{AP}{AQ}$=$\sqrt{2}$ | D. | 当x•y=4时,AB=4 |
4.已知点A的坐标为(a,b),O为坐标原点,连结OA,将线段OA绕点O按逆时针方向旋转180°得OA1,则点A1的坐标为( )
| A. | (-a,b) | B. | (a,-b) | C. | (-a,-b) | D. | (b,-a) |
9.|1-$\sqrt{2}$|的相反数为( )
| A. | 1-$\sqrt{2}$ | B. | $\sqrt{2}$-1 | C. | 1+$\sqrt{2}$ | D. | -1-$\sqrt{2}$ |
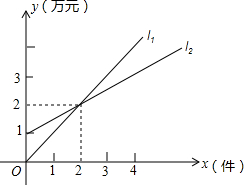 如图,l1表示某个公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.
如图,l1表示某个公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.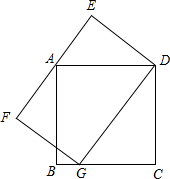 已知:如图,正方形的顶点A在矩形DEFG的边EF上,矩形DEFG的顶点G在正方形的边BC上,正方形的边长为4,DG的长为6,则DE的长为$\frac{8}{3}$.
已知:如图,正方形的顶点A在矩形DEFG的边EF上,矩形DEFG的顶点G在正方形的边BC上,正方形的边长为4,DG的长为6,则DE的长为$\frac{8}{3}$.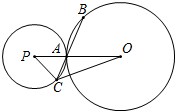 如图,已知⊙O的半径为5,⊙P与⊙O外切于点A,经过点A的直线与⊙O、⊙P分别交于点B、C,tan∠OAB=$\frac{\sqrt{21}}{2}$.
如图,已知⊙O的半径为5,⊙P与⊙O外切于点A,经过点A的直线与⊙O、⊙P分别交于点B、C,tan∠OAB=$\frac{\sqrt{21}}{2}$.