题目内容
3.已知二次函数y=-x2+bx+c的图象的对称轴为直线x=-1,设图象与x轴交于点(x1,0)、(x2,0),若x12+x22=10,试求此函数的解析式.分析 先利用抛物线对称轴方程可求出b=-2,再根据抛物线与x轴的交点问题得到方程-x2-2x+c=0的两根为x1,x2,利用根与系数的关系得到x1+x2=-2,x1•x2=-c,加上x12+x22=10,通过消去x1,x2可求出c的值,从而得到抛物线解析式.
解答 解:∵抛物线的对称轴为直线x=-$\frac{b}{2×(-1)}$=-1,
∴b=-2,
∴y=-x2-2x+c,
∵抛物线与x轴交于点(x1,0)、(x2,0),
∴方程-x2-2x+c=0的两根为x1,x2,
∴x1+x2=-2,x1•x2=-c,
∵x12+x22=10,
∴(x1+x2)2-2x1•x2=10,
∴(-2)2+2c=10,解得c=3,
∴抛物线的解析式为y=-x2-2x+3.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标转化为解关于x的一元二次方程.也考查了根与系数的关系.

练习册系列答案
相关题目
 如图,AP∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的延长线交AP于D.
如图,AP∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的延长线交AP于D.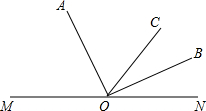 如图,点M,O,N在同一直线上,射线OA和射线OB分别平分∠MOC和∠NOC,∠AOB是什么角?请说明理由.
如图,点M,O,N在同一直线上,射线OA和射线OB分别平分∠MOC和∠NOC,∠AOB是什么角?请说明理由.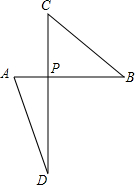 如图,点P是线段AB的黄金分割点,将线段PB绕着点P逆时针旋转90°到点C,延长CP到点D.使PD=AB.连接AD,试比较△PCB与△PAD的面积大小,并说明理由.
如图,点P是线段AB的黄金分割点,将线段PB绕着点P逆时针旋转90°到点C,延长CP到点D.使PD=AB.连接AD,试比较△PCB与△PAD的面积大小,并说明理由.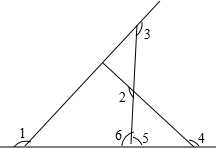 如图,求∠1+∠2+∠3+∠4的度数.
如图,求∠1+∠2+∠3+∠4的度数. 如图,DE∥AC,CD平分∠ACB,EF平分∠BED.
如图,DE∥AC,CD平分∠ACB,EF平分∠BED. 如图所示,在一个水塘的表面均匀漂浮一些鱼食,一只小鱼正在A出,现在小鱼从A处出发到到水面取一点食物后,要回到岸边的B洞口处,画出小鱼这一过程中游动的最短路径(请保留作图中必要的辅助线).
如图所示,在一个水塘的表面均匀漂浮一些鱼食,一只小鱼正在A出,现在小鱼从A处出发到到水面取一点食物后,要回到岸边的B洞口处,画出小鱼这一过程中游动的最短路径(请保留作图中必要的辅助线).