题目内容
13. 如图,AP∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的延长线交AP于D.
如图,AP∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的延长线交AP于D.(1)思考AE与BE的位置关系并加以说明;
(2)说明AB=AD+BC;
(3)若BE=6,AE=6.5,求四边形ABCD的面积?
分析 (1)根据平行线的性质得出∠DAB+∠CBA=180°,再利用角平分线的定义和三角形的内角和解答即可;
(2)此题要通过构造全等三角形来求解,延长AE交BC的延长线于M;由AP∥BC,及AE平分∠PAB,可求得∠BAE=∠M,即AB=BM,因此直线证得AD=MC即可;在等腰△ABM中,BE是顶角的平分线,根据等腰三角形三线合一的性质知:E是AM的中点,即AE=EM,而PA∥BM,即可证得△ADE≌△MCE,从而得到所求的结论.
(3)由(2)的全等三角形可知:△ADE、△MCE的面积相等,从而将所求四边形的面积转化为等腰△ABM的面积,易得AM、BE的值,从而根据三角形的面积公式求得△ABM的面积,即四边形ADCB的面积.
解答 (1)解:AE与BE垂直,理由如下:
∵AP∥BC,
∴∠DAB+∠CBA=180°,
∵∠PAB的平分线与∠CBA的平分线相交于E,
∴∠EAB+∠EBA=90°,
∴∠AEB=90°,
∴AE⊥EB;
(2)证明:延长AE交BC的延长线于M,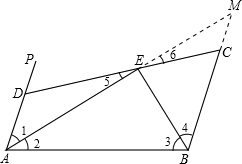
∵AE平分∠PAB,BE平分∠CBA,
∴∠1=∠2,∠3=∠4,
∵AD∥BC
∴∠1=∠M=∠2,∠1+∠2+∠3+∠4=180°
∴BM=BA,∠3+∠2=90°,
∴BE⊥AM,
在△ABE和△MBE中,
$\left\{\begin{array}{l}{∠3=∠4}\\{BE=BE}\\{∠AEB=∠MEB}\end{array}\right.$,
∴△ABE≌△MBE
∴AE=ME,
在△ADE和△MCE中,
$\left\{\begin{array}{l}{∠1=∠M}\\{AE=ME}\\{∠5=∠6}\end{array}\right.$;
∴△ADE≌△MCE,
∴AD=CM,
∴AB=BM=BC+AD.
(3)解:由(2)知:△ADE≌△MCE,
∴S四边形ABCD=S△ABM
又∵AE=ME=6.5,BE=6,
∴${S}_{△ABM}=\frac{1}{2}×13×6=39$,
∴S四边形ABCD=39.
点评 此题主要考查的是全等三角形的判定和性质,同时还涉及了角平分线定义、平行线的性质以及等腰三角形的性质,正确地构造出全等三角形是解答此题的关键.

 两数在数轴上表示如图所示,则下列结论错误的是( )
两数在数轴上表示如图所示,则下列结论错误的是( )| A. | a-b<0 | B. | ab<0 | C. | -b>a | D. | a+b<0 |
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |