题目内容
15.2015年10月11日中国新闻网报道,在故官博物院“石渠宝笺展”真迹展出之际,荣宝斋主办的“石渠宝笺”高仿真艺术品在内蒙古举行首展,某商场购进某种仿真工艺品,已知每件工艺品的进价为40元,在销售过程中发现月销量y(件)与销售单价x(元)成一次函数关系,并且当销售单价为70元时,每月销量可达50件,当销售单价为90元时,每月销量可达30件,每月销售该工艺品的其他支出为300元.(1)写出该产品月利润p(元)与销售单价x(元)之间的函数表达式;(月利润=总销售额-进价-其他支出)
(2)求当销售单价为多少时,月利润最大?最大利润是多少?
(3)若该商场每月的利润不低于675元,在此条件下要使产品的销量最大,求销售单价应定为多少?
分析 (1)设y与x的函数关系式y=kx+b,根据售价与销量之间的数量关系建立方程组,月销量y(件)与销售单价x(元)的函数关系,然后根据月利润=总销售额-进价-其它支出求出,该产品月利润p(元)与销售单价x(元)之间的函数表达式;
(2)根据利润=(售价-进价)×数量就可以表示出p;
(3)求出年销售获利等于675万元时,销售单价x的值,从而确定销售单价x的范围,及二次函数w最大时,x的值.
解答 解:(1)设月销量y(件)与销售单价x(元)成一次函数关系为y=kx+b,
则$\left\{\begin{array}{l}{50=70k+b}\\{30=90k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=120}\end{array}\right.$.
∴月销量y(件)与销售单价x(元)成一次函数关系为:y=-x+120,
∴p=(-x+120)(x-40)-300=-x2+160x-5100;
(2)∵p=-x2+160x-5100=-(x-80)2+1300,
∴当x=80时,p最大=1300,
即:销售单价为80元时,月利润最大,最大利润是1300元;
(3)令p=675,得-x2+160x-5100=675,
整理,得x2-160x+5775=0.
解得x1=105,x2=55.
要使年获利不低于675万元,销售单价应在55元到105元之间.
又因为销售单价越低,销售量越大,
所以要使销售量最大,又使年获利不低于675万元,销售单价应定为55元.
点评 此题主要考查了二次函数的应用,一元二次方程的应用,关键是正确理解题意,找出题目中的等量关系,掌握售价-进价=利润.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 如图,P是反比例函数y=$\frac{9}{2x}$(k>0)第一象限的图象上的一点,则P到原点的最小距离为3.
如图,P是反比例函数y=$\frac{9}{2x}$(k>0)第一象限的图象上的一点,则P到原点的最小距离为3. 如图,抛物线y=ax2+b与x轴交于点A,B,且A点的坐标为(1,0),与y轴交于点C(0,1)
如图,抛物线y=ax2+b与x轴交于点A,B,且A点的坐标为(1,0),与y轴交于点C(0,1)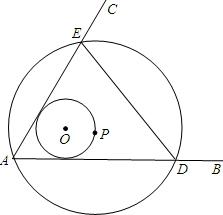 如图∠BAC=60°,半径长1的⊙0与∠BAC的两边相切,P为⊙O上一动点,以P为圆心,PA长为半径的⊙P交射线AB、AC于D、E两点,连接DE,则△EDA面积的最大值为$\frac{27\sqrt{3}}{4}$.
如图∠BAC=60°,半径长1的⊙0与∠BAC的两边相切,P为⊙O上一动点,以P为圆心,PA长为半径的⊙P交射线AB、AC于D、E两点,连接DE,则△EDA面积的最大值为$\frac{27\sqrt{3}}{4}$.