题目内容
13.已知xyz=1,求证:$\frac{1}{xy+y+1}$+$\frac{1}{yz+z+1}$+$\frac{1}{xz+x+1}$=1.分析 根据xyz=1,以及分式的基本性质把等式左边的三个分式化成分母相同的形式,然后相加即可证明.
解答 证明:$\frac{1}{xy+y+1}$+$\frac{1}{yz+z+1}$+$\frac{1}{xz+x+1}$
=$\frac{1}{xy+y+1}$+$\frac{xy}{xy•yz+xyz+xy}$+$\frac{y}{xyz+xy+y}$
=$\frac{1}{xy+y+1}$+$\frac{xy}{y+1+xy}$+$\frac{y}{1+xy+y}$
=$\frac{xy+y+1}{xy+y+1}$
=1.
点评 本题考查了分式的化简求值,正确对所求的分式进行变形是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.在某复印社复印文件,复印页数不超过50时,每页收费0.11元,超过部分每页收费降为0.08元.在某图书馆复印同样的文件,不论复印多少页,每页收费0.09元.
设需要复印文件x页(x为正整数),请根据表中提供的信息回答下列问题:
(1)用含有x的式子填写如表:
(2)当x为何值时,两种收费相等;
(3)当你有一本书要复印、页码共有200页,你认为在哪里复印省钱?(直接写出结果即可)
设需要复印文件x页(x为正整数),请根据表中提供的信息回答下列问题:
(1)用含有x的式子填写如表:
| x≤50 | x>50 | |
| 复印店计费/元 | 0.11x | 0.08x+1.5 |
| 图书馆计费/元 | 0.09x | 0.09x |
(3)当你有一本书要复印、页码共有200页,你认为在哪里复印省钱?(直接写出结果即可)
18.已知点A(x,y-4)与点B(1-y,2x)关于原点对称,则yx的值是( )
| A. | 2 | B. | 1 | C. | 4 | D. | 8 |
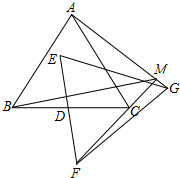 如图,△ABC、△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最大值是$\sqrt{3}$+1.
如图,△ABC、△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最大值是$\sqrt{3}$+1. 如图,从一个直径为4的圆形铁片中剪下一个圆心角为90°的扇形ABC.求这个扇形的面积.
如图,从一个直径为4的圆形铁片中剪下一个圆心角为90°的扇形ABC.求这个扇形的面积.