题目内容
11.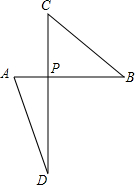 如图,点P是线段AB的黄金分割点,将线段PB绕着点P逆时针旋转90°到点C,延长CP到点D.使PD=AB.连接AD,试比较△PCB与△PAD的面积大小,并说明理由.
如图,点P是线段AB的黄金分割点,将线段PB绕着点P逆时针旋转90°到点C,延长CP到点D.使PD=AB.连接AD,试比较△PCB与△PAD的面积大小,并说明理由.
分析 根据旋转的性质得PC=PB,∠CPB=90°,则利用三角形面积公式得到S△PCB=$\frac{1}{2}$PB•PC=$\frac{1}{2}$PB2,S△PAD=$\frac{1}{2}$AP•PD,由于PD=AB,所以S△PAD=$\frac{1}{2}$AP•AB,接着根据黄金分割的定义有PB2=AP•AB,所以S△PCB=S△PAD.
解答 解:△PCB与△PAD的面积相等.理由如下:
∵线段PB绕着点P逆时针旋转90°到点C,
∴PC=PB,∠CPB=90°,
∵S△PCB=$\frac{1}{2}$PB•PC=$\frac{1}{2}$PB2,S△PAD=$\frac{1}{2}$AP•PD,
∵PD=AB,
∴S△PAD=$\frac{1}{2}$AP•AB,
∵点P是线段AB的黄金分割点,
∴PB:AB=AP:PB,
即PB2=AP•AB,
∴S△PCB=S△PAD.
点评 本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫作把线段AB黄金分割,点C叫作线段AB的黄金分割点.其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB,并且线段AB的黄金分割点有两个.也考查了旋转的性质.

练习册系列答案
相关题目
1.在某复印社复印文件,复印页数不超过50时,每页收费0.11元,超过部分每页收费降为0.08元.在某图书馆复印同样的文件,不论复印多少页,每页收费0.09元.
设需要复印文件x页(x为正整数),请根据表中提供的信息回答下列问题:
(1)用含有x的式子填写如表:
(2)当x为何值时,两种收费相等;
(3)当你有一本书要复印、页码共有200页,你认为在哪里复印省钱?(直接写出结果即可)
设需要复印文件x页(x为正整数),请根据表中提供的信息回答下列问题:
(1)用含有x的式子填写如表:
| x≤50 | x>50 | |
| 复印店计费/元 | 0.11x | 0.08x+1.5 |
| 图书馆计费/元 | 0.09x | 0.09x |
(3)当你有一本书要复印、页码共有200页,你认为在哪里复印省钱?(直接写出结果即可)
 如图,P是反比例函数y=$\frac{9}{2x}$(k>0)第一象限的图象上的一点,则P到原点的最小距离为3.
如图,P是反比例函数y=$\frac{9}{2x}$(k>0)第一象限的图象上的一点,则P到原点的最小距离为3. 如图,抛物线y=ax2+b与x轴交于点A,B,且A点的坐标为(1,0),与y轴交于点C(0,1)
如图,抛物线y=ax2+b与x轴交于点A,B,且A点的坐标为(1,0),与y轴交于点C(0,1)