Question

1．在平面直角坐标系xOy中，点M的坐标为（m，1）．如果以原点为圆心，半径为1的⊙O上存在点N，使得∠OMN=45°，那么m的取值范围是（　　）

• A． -1≤m≤1
• B． -1＜m＜1
• C． 0≤m≤1
• D． 0＜m＜1

Answer 1

分析 令⊙O与x轴的交点为N₁、N₂，过点N₁、N₂分别做N₁M₁、N₂M₂垂直于直线y=1于点M₁、M₂，根据⊙O的半径为1即可找出N₁、N₂、M₁、M₂的坐标，再结合在半径为1的⊙O上存在点N，使得∠OMN=45°，即可得出点M在线段M₁M₂上，从而得出m的取值范围．

解答 解：令⊙O与x轴的交点为N₁、N₂，过点N₁、N₂分别做N₁M₁、N₂M₂垂直于直线y=1于点M₁、M₂，如图所示．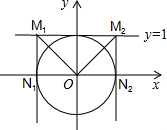
则点N₁（-1，0）、N₂（1，0），M₁（-1，1），M₂（1，1），
∵在半径为1的⊙O上存在点N，使得∠OMN=45°，
∴点M在线段M₁M₂上，
∴-1≤m≤1．
故选A．

点评 本题考查了坐标与图形的性质，解题的关键是找出点M在线段M₁M₂上．本题属于基础题，难度不大，解决该题型题目时，画出图形利用数形结合解决问题是关键．