题目内容

8．在-1.732，$\sqrt{2}$，π，3.14，2+$\sqrt{3}$，3.212212221…，3.14这些数中，无理数的个数为（　　）
A．5B．2C．3D．4

分析 根据无理数的定义：无限不循环小数，据此即可判断．

解答 解：无理数有：$\sqrt{2}$，2+$\sqrt{3}$，3.212212221…共3个．
故选C．

点评 此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，$\sqrt{6}$，0.8080080008…（每两个8之间依次多1个0）等形式．

练习册系列答案
相关题目
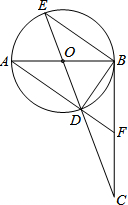18．如图，AB是⊙O的直径，BC⊥AB，垂足为点B，连接CO并延长交⊙O于点D、E，连接AD并延长交BC于点F．则下列结论正确的有（　　）
①∠CBD=∠CEB；②$\frac{BD}{BE}$=$\frac{CD}{BC}$；③点F是BC的中点；④若$\frac{BC}{AB}$=$\frac{3}{2}$，tanE=$\frac{\sqrt{10}-1}{3}$．
A．1B．2C．3D．4
19．数学课上，在将一个二次三项式进行因式分解时，刘老师巡视发现甲、乙同学的解题过程都正确，但答案都错了．甲同学的错误答案是2（x-1）（x-9），错因是看错了一次项系数；乙同学的错误答案是2（x-2）（x-4），错因是看错了常数项．请将原多项式因式分解．
16．81的平方根是±9，9的算术平方根是3，-27的立方根是-3．
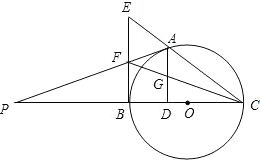3．如图，点A是以BC为直径的⊙O上一点，AD⊥BC于点D，过点B作⊙O的切线，与CA的延长线相交于点E，G是AD的中点，连结CG并延长与BE相交于点F，延长AF与CB的延长线相交于点P，且FG=FB=3．则以下四个结论：①BF=EF；②PA⊥OA；③tan∠P=$\frac{{\sqrt{2}}}{3}$；④OC=3$\sqrt{2}$，上述结论中正确的有①②④（填番号）．
13．下列说法正确的是（　　）
A．平角是一条直线B．角的边越长，角越大
C．大于直角的角叫做钝角D．两个锐角的和不一定是钝角
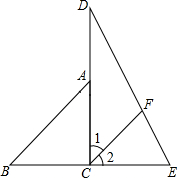20．将一副直角三角尺拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F，试判断CF与AB是否平行，并说明理由．
17．已知：a=$\frac{1}{2-\sqrt{3}}$，b=$\frac{1}{2+\sqrt{3}}$，则a与b的关系是（　　）
A．ab=1B．a+b=0C．a-b=0D．a2=b2
18．解方程（组）：
（1）$\left\{\begin{array}{l}{2x-y=5①}\\{x-1=\frac{1}{2}（2y-1）②}\end{array}\right.$  
（2）$\frac{x+1}{x-1}-\frac{4}{{{x^2}-1}}=1$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网