题目内容
12. 如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{BC}$,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是( )
如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{BC}$,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是( )| A. | $\frac{5}{3}π-2\sqrt{3}$ | B. | $\frac{5}{3}π+2\sqrt{3}$ | C. | 2$\sqrt{3}-\frac{5}{3}π$ | D. | $\sqrt{3}+\frac{5}{3}π$ |
分析 如图,连接CE.图中S阴影=S扇形BCE-S扇形BOD-S△OCE.根据已知条件易求得OB=OC=OD=2,BC=CE=4.∠ECB=60°,OE=2$\sqrt{3}$所以由扇形面积公式、三角形面积公式进行解答即可.
解答  解:如图,连接CE.
解:如图,连接CE.
∵AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB,
∴∠ACB=90°,OB=OC=OD=2,BC=CE=4.
又∵OE∥AC,
∴∠ACB=∠COE=90°.
∴在直角△OEC中,OC=2,CE=4,
∴∠CEO=30°,∠ECB=60°,OE=2$\sqrt{3}$
∴S阴影=S扇形BCE-S扇形BOD-S△OCE=$\frac{60π×{4}^{2}}{360}$-$\frac{1}{4}$π×22-$\frac{1}{2}$×2×2$\sqrt{3}$=$\frac{5π}{3}$-2$\sqrt{3}$,
故选A.
点评 本题考查了扇形面积的计算.不规则图形的面积一定要注意分割成规则图形的面积进行计算.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
7.若a=b-3,则b-a的值是( )
| A. | -3 | B. | 3 | C. | 0 | D. | 6 |
17.已知:a=$\frac{1}{2-\sqrt{3}}$,b=$\frac{1}{2+\sqrt{3}}$,则a与b的关系是( )
| A. | ab=1 | B. | a+b=0 | C. | a-b=0 | D. | a2=b2 |
1.下列美丽的图案,既是轴对称图形又是中心对称图形的个数是( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 甲、乙两车分别从M,N两地沿同一公路相向匀速行驶,两车分别抵达N,M两地后即停止行驶.已知乙车比甲车提前出发,设甲、乙两车之间的路程S(km),乙行驶的时间为t(h),S与t的函数关系如图所示.有下列说法:
甲、乙两车分别从M,N两地沿同一公路相向匀速行驶,两车分别抵达N,M两地后即停止行驶.已知乙车比甲车提前出发,设甲、乙两车之间的路程S(km),乙行驶的时间为t(h),S与t的函数关系如图所示.有下列说法: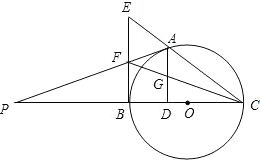 如图,点A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P,且FG=FB=3.则以下四个结论:①BF=EF;②PA⊥OA;③tan∠P=$\frac{{\sqrt{2}}}{3}$;④OC=3$\sqrt{2}$,上述结论中正确的有①②④(填番号).
如图,点A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P,且FG=FB=3.则以下四个结论:①BF=EF;②PA⊥OA;③tan∠P=$\frac{{\sqrt{2}}}{3}$;④OC=3$\sqrt{2}$,上述结论中正确的有①②④(填番号).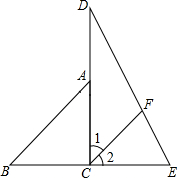 将一副直角三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.
将一副直角三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.