题目内容
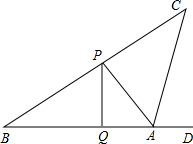 AC是一条不能行走的斜坡,为了测量斜坡AC的长度,在一次课外实践活动中.小明所在的活动小组进行了以下的操作:首先在AB之间插一根12米高的旗杆PQ,他们在B处测得旗杆顶点P的仰角为30°,在A处测得旗杆顶点P的仰角为45°,在A处测得斜坡的末端C点的仰角为75°.
AC是一条不能行走的斜坡,为了测量斜坡AC的长度,在一次课外实践活动中.小明所在的活动小组进行了以下的操作:首先在AB之间插一根12米高的旗杆PQ,他们在B处测得旗杆顶点P的仰角为30°,在A处测得旗杆顶点P的仰角为45°,在A处测得斜坡的末端C点的仰角为75°.(1)求A、B之间的距离;
(2)求斜坡AC的长度.
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:(1)先根据PQ=12m,∠B=30°求出BQ的长,再由∠PAB=45°求出AQ的长,根据AB=BQ+AQ即可得出结论;
(2)过A作AE⊥BC于E,先根据直角三角形的性质求出AE的长,再由三角形外角的性质得出∠C的度数,根据直角三角形的性质即可得出结论.
(2)过A作AE⊥BC于E,先根据直角三角形的性质求出AE的长,再由三角形外角的性质得出∠C的度数,根据直角三角形的性质即可得出结论.
解答: 解:(1)∵PQ=12m,∠B=30°,PQ⊥AB,
解:(1)∵PQ=12m,∠B=30°,PQ⊥AB,
∴BQ=
=
=12
.
在Rt△AQP中,
∵∠PAQ=45°,
∴AQ=PQ=12,
∴AB=BQ+AQ=(12
+12)(米);
(2)过A作AE⊥BC于E,
∵∠B=30°,
∴AE=
AB=6+6
.
∵∠CAD=75°,∠B=30°,
∴∠C=75°-30°=45°,
∴AC=
=
=(6
+6
)(米).
 解:(1)∵PQ=12m,∠B=30°,PQ⊥AB,
解:(1)∵PQ=12m,∠B=30°,PQ⊥AB,∴BQ=
| PQ |
| tan30° |
| 12 | ||||
|
| 3 |
在Rt△AQP中,
∵∠PAQ=45°,
∴AQ=PQ=12,
∴AB=BQ+AQ=(12
| 3 |
(2)过A作AE⊥BC于E,
∵∠B=30°,
∴AE=
| 1 |
| 2 |
| 3 |
∵∠CAD=75°,∠B=30°,
∴∠C=75°-30°=45°,
∴AC=
| AE |
| sin45° |
6+6
| ||||
|
| 2 |
| 6 |
点评:本题考查的是解直角三角形的应用-仰角俯角问题,熟知锐角三角函数的定义是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
分解因式9-(5x-2y)2正确的是( )
| A、(9+5x-2y)(9-5x+2y) |
| B、(3+5x-2y)(3-5x-2y) |
| C、(3+5x-2y)(3-5x+2y) |
| D、(3+5x+2y)(3-5x+2y) |
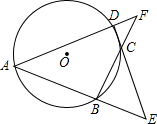 如图,A、B、C、D为⊙O上四点,AB、DC交于E点,AD、BC交于点F.若∠E=36°,∠F=30°,则∠A的度数为( )
如图,A、B、C、D为⊙O上四点,AB、DC交于E点,AD、BC交于点F.若∠E=36°,∠F=30°,则∠A的度数为( )| A、30° | B、40° |
| C、57° | D、70° |
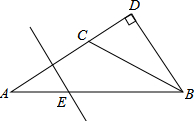 如图,△ABD中∠D=90°,C为AD上一点,且AC=BC=2CD,AC的垂直平分线交AB于E,求
如图,△ABD中∠D=90°,C为AD上一点,且AC=BC=2CD,AC的垂直平分线交AB于E,求 如图,在△ABC中.AB=AC,AB的垂直平分线交直线AB于点N,交直线BC于点M.若∠A=40°,求∠NMB的大小.
如图,在△ABC中.AB=AC,AB的垂直平分线交直线AB于点N,交直线BC于点M.若∠A=40°,求∠NMB的大小.