题目内容
观察:
+
+
=(
-
)+(
-
)+(
-
)=1-
=
(1)计算:
+
+
+…+
(2)计算:
+
+
+…+
(n为正整数)
(3)拓展应用:
①解方程:
+
+
+
+
=
②计算:
+
+
+
+
.
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
(1)计算:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 9×10 |
(2)计算:
| 3 |
| 1×2 |
| 3 |
| 2×3 |
| 3 |
| 3×4 |
| 3 |
| n×(n+1) |
(3)拓展应用:
①解方程:
| 1 |
| (x-4)(x-3) |
| 1 |
| (x-3)(x-2) |
| 1 |
| (x-2)(x-1) |
| 1 |
| (x-1)x |
| 1 |
| x(x+1) |
| 1 |
| x+1 |
②计算:
| 1 |
| 1×4 |
| 1 |
| 4×7 |
| 1 |
| 7×10 |
| 1 |
| 10×13 |
| 1 |
| 13×16 |
考点:分式的加减法,解分式方程
专题:规律型
分析:(1)根据已知等式得出拆项规律,原式计算即可得到结果;
(2)原式提取3后,利用拆项法计算即可得到结果;
(3)①方程左边利用拆项法变形后,计算即可求出解;
②原式变形后,利用拆项法计算即可得到结果.
(2)原式提取3后,利用拆项法计算即可得到结果;
(3)①方程左边利用拆项法变形后,计算即可求出解;
②原式变形后,利用拆项法计算即可得到结果.
解答:解:(1)原式=1-
+
-
+…+
-
=1-
=
;
(2)原式=3(1-
+
-
+…+
-
)=3(1-
)=
;
(3)①方程变形得:
-
+
-
+
-
+
-
+
-
=
,
整理得:
=
,
去分母得:x+1=2x-8,
解得:x=9,
经检验x=9是分式方程的解;
②原式=
(1-
+
-
+…+
-
)=
(1-
)=
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| 10 |
| 9 |
| 10 |
(2)原式=3(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 3n |
| n+1 |
(3)①方程变形得:
| 1 |
| x-4 |
| 1 |
| x-3 |
| 1 |
| x-3 |
| 1 |
| x-2 |
| 1 |
| x-2 |
| 1 |
| x-1 |
| 1 |
| x-1 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x+1 |
| 1 |
| x+1 |
整理得:
| 1 |
| x-4 |
| 2 |
| x+1 |
去分母得:x+1=2x-8,
解得:x=9,
经检验x=9是分式方程的解;
②原式=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 7 |
| 1 |
| 13 |
| 1 |
| 16 |
| 1 |
| 3 |
| 1 |
| 16 |
| 5 |
| 16 |
点评:此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
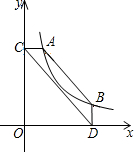 如图,点A、B在反比例函数y=
如图,点A、B在反比例函数y=| 8 |
| x |
| A、AB与CD平行 |
| B、AB与CD相交 |
| C、AB与CD平行或相交 |
| D、以上答案都不对 |
 如图,已知AD⊥BC于D,BG⊥BC于G,AE=AF,说明AD平分∠BAC,下面是小颖的解答过程,请补充完整.
如图,已知AD⊥BC于D,BG⊥BC于G,AE=AF,说明AD平分∠BAC,下面是小颖的解答过程,请补充完整. 如图:
如图: