题目内容
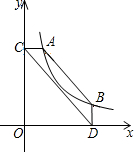 如图,点A、B在反比例函数y=
如图,点A、B在反比例函数y=| 8 |
| x |
| A、AB与CD平行 |
| B、AB与CD相交 |
| C、AB与CD平行或相交 |
| D、以上答案都不对 |
考点:反比例函数综合题,矩形的判定与性质,比例的性质,相似三角形的判定与性质
专题:探究型
分析:由于点A、B是反比例函数图象的动点,因此可分点A在点B的左边、右边两种情况讨论.易证四边形OCED是矩形,从而有OC=ED,OD=CE.设AC=a,OC=b,OD=c,BD=d,则A(a,b),B(c,d).由点A,B在反比例函数y=
的图象上得到AC•OC=OD•BD,从而有AC•ED=CE•BD,进而可以证到△AEB∽△CED,就可得到∠EAB=∠ECD,则有AB∥CD.
| 8 |
| x |
解答:解:①若点A在点B的左边,延长CA、DB交于点E,如图1,
∵AC⊥y轴,BD⊥x轴,∠COD=90°,
∴∠OCE=∠COD=∠ODE=90°.
∴四边形OCED是矩形.
∴OC=ED,OD=CE.
设AC=a,OC=b,OD=c,BD=d,
则A(a,b),B(c,d).
∵点A(a,b),B(c,d)在反比例函数y=
的图象上,
∴ab=cd=8.
∴AC•OC=OD•BD.
∴AC•ED=CE•BD.
∴
=
.
∴
=
.
∵∠AEB=∠CED,
∴△AEB∽△CED.
∴∠EAB=∠ECD.
∴AB∥CD.
②若点A在点B的右边,如图2,
同理可得:AB∥CD.
综上所述:AB始终与CD平行.
故选:A.

∵AC⊥y轴,BD⊥x轴,∠COD=90°,
∴∠OCE=∠COD=∠ODE=90°.
∴四边形OCED是矩形.
∴OC=ED,OD=CE.
设AC=a,OC=b,OD=c,BD=d,
则A(a,b),B(c,d).
∵点A(a,b),B(c,d)在反比例函数y=
| 8 |
| x |
∴ab=cd=8.
∴AC•OC=OD•BD.
∴AC•ED=CE•BD.
∴
| AC |
| CE |
| BD |
| ED |
∴
| AE |
| CE |
| EB |
| ED |

∵∠AEB=∠CED,
∴△AEB∽△CED.
∴∠EAB=∠ECD.
∴AB∥CD.
②若点A在点B的右边,如图2,
同理可得:AB∥CD.
综上所述:AB始终与CD平行.
故选:A.
点评:本题考查了反比例函数图象上的点坐标特征、相似三角形的判定与性质、矩形的判定与性质、比例的性质等知识,考查了分类讨论的思想,是一道好题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
用反证法证明命题“一个三角形中至少有一个角不小于60度”,应先假设这个三角形中( )
| A、至多有两个角小于60度 |
| B、都小于60度 |
| C、至少有一个角是小于60度 |
| D、都大于60度 |
下列函数中,y的值随x的增大而增大的是( )
A、y=-
| ||
| B、y=-x-2 | ||
C、y=
| ||
| D、y=-3x |
 如图,矩形ABCD中,对角线AC、BD相交于点0,在BC上取BE=BO,连结AE,OE.若∠BOE=75°,则∠CAE的度数等于( )
如图,矩形ABCD中,对角线AC、BD相交于点0,在BC上取BE=BO,连结AE,OE.若∠BOE=75°,则∠CAE的度数等于( )| A、30° | B、45° |
| C、20° | D、15 |
方程组
的解是( )
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
如图是甲、乙两地某年财政经费支出情况统计图,阴影部分表示教育经费支出.从中可以看出( )

| A、甲地教育经费占财政经费支出比率较高 |
| B、甲地教育经费支出比较多 |
| C、甲地教育经费支出增幅比较大 |
| D、甲地财政经费支出总额比较小 |