题目内容
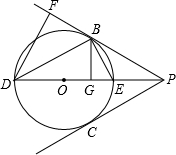 如图,PB、PC分别切⊙O于B、C,DE是圆的直径.
如图,PB、PC分别切⊙O于B、C,DE是圆的直径.(1)若tanD=
| 1 |
| 2 |
(2)过点D作DF⊥PB于F,探索DF、DE、DB之间的关系;
(3)过点B作BG⊥DE于G,探索BE与FG之间的关系.
考点:切线的性质
专题:证明题
分析:(1)连结OB,作BG⊥DE于G,如图,根据圆周角定理由DE是圆的直径得到∠DBE=90°,在Rt△BDE中,利用正切的定义得到DB=2BE,根据勾股定理可计算出BE=
,则DB=
,接着利用面积法计算出BG=
;则在Rt△OBG中利用勾股定理可计算出OG=
,然后证明△OBG∽△OPB,利用相似比计算出OP=10,最后在Rt△OPB中再根据勾股定理可计算出PB;
(2)证明△DFG∽Rt△DBE,利用相似比可得到BD2=DF•DE;
(3)先证明△DFB≌△DGB得到DF=DG,加上BD平分∠FDG,则可根据等腰三角形的性质得到BD⊥FG,然后根据平行线的判定即可得到BE∥FG.
12
| ||
| 5 |
24
| ||
| 5 |
| 24 |
| 5 |
| 18 |
| 5 |
(2)证明△DFG∽Rt△DBE,利用相似比可得到BD2=DF•DE;
(3)先证明△DFB≌△DGB得到DF=DG,加上BD平分∠FDG,则可根据等腰三角形的性质得到BD⊥FG,然后根据平行线的判定即可得到BE∥FG.
解答: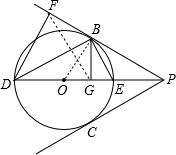 解:(1)连结OB,作BG⊥DE于G,如图,
解:(1)连结OB,作BG⊥DE于G,如图,
∵DE是圆的直径,
∴∠DBE=90°,
在Rt△BDE中,∵tan∠BDE=
=
,
∴DB=2BE,
∵BE2+DB2=DE2,
∴BE2+4BE2=122,解得BE=
,
∴DB=
,
∵
BG•DE=
DB•BE,
∴BG=
,
在Rt△OBG中,OG=
=
,
∵∠BOG=∠POB,
∴△OBG∽△OPB,
∴OB:OP=OG:OB,即6:OP=
:6,
∴OP=10,
在Rt△OPB中,∵OB=6,OP=10,
∴PB=
=8;
(2)∵DF⊥PB,OB∥PB,
∴OB∥DF,
∴∠FDB=∠OBD,
而OB=OD,
∴∠ODB=∠OBD,
∴∠FDB=∠ODB,
∴Rt△DFG∽Rt△DBE,
∴DF:BD=BD:DE,
∴BD2=DF•DE;
(3)在△DFB和△DGB中,
,
∴△DFB≌△DGB(AAS),
∴DF=DG,
∵BD平分∠FDG,
∴BD⊥FG,
∵BD⊥BE,
∴BE∥FG.
 解:(1)连结OB,作BG⊥DE于G,如图,
解:(1)连结OB,作BG⊥DE于G,如图,∵DE是圆的直径,
∴∠DBE=90°,
在Rt△BDE中,∵tan∠BDE=
| BE |
| DB |
| 1 |
| 2 |
∴DB=2BE,
∵BE2+DB2=DE2,
∴BE2+4BE2=122,解得BE=
12
| ||
| 5 |
∴DB=
24
| ||
| 5 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴BG=
| 24 |
| 5 |
在Rt△OBG中,OG=
| OB2-BG2 |
| 18 |
| 5 |
∵∠BOG=∠POB,
∴△OBG∽△OPB,
∴OB:OP=OG:OB,即6:OP=
| 18 |
| 5 |
∴OP=10,
在Rt△OPB中,∵OB=6,OP=10,
∴PB=
| OP2-OB2 |
(2)∵DF⊥PB,OB∥PB,
∴OB∥DF,
∴∠FDB=∠OBD,
而OB=OD,
∴∠ODB=∠OBD,
∴∠FDB=∠ODB,
∴Rt△DFG∽Rt△DBE,
∴DF:BD=BD:DE,
∴BD2=DF•DE;
(3)在△DFB和△DGB中,
|
∴△DFB≌△DGB(AAS),
∴DF=DG,
∵BD平分∠FDG,
∴BD⊥FG,
∵BD⊥BE,
∴BE∥FG.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了相似三角形的判定与性质.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
如图,从边长为(a+4)的正方形纸片中剪去一个边长为(a+1)的正方形(a>0),剩余部分沿虚线又剪拼成一个长方形(不重叠、无缝隙),若拼成的长方形一边的长为3,则另一边的长为( )
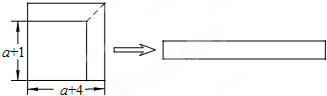

| A、2a+5 | B、2a+8 |
| C、2a+3 | D、2a+2 |
 CE是△ABC的外角∠ACD的平分线,AB的垂直平分线FG分别交AB,CE于F,G.联结GA,GB.求证:∠GAC=∠GBC.
CE是△ABC的外角∠ACD的平分线,AB的垂直平分线FG分别交AB,CE于F,G.联结GA,GB.求证:∠GAC=∠GBC. 如图,在平面直角坐标系中,四边形ABCD各顶点坐标分别为A(0,3),B(2,4),C(4,3),D(2,1).
如图,在平面直角坐标系中,四边形ABCD各顶点坐标分别为A(0,3),B(2,4),C(4,3),D(2,1).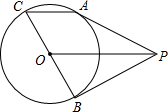 已知,如图,点P在⊙O外,PA、PB是⊙O的切线,A、B为切点,BC是直径,连接CA.求证:CA∥OP.
已知,如图,点P在⊙O外,PA、PB是⊙O的切线,A、B为切点,BC是直径,连接CA.求证:CA∥OP.