题目内容
已知二次函数图象的顶点坐标是(-2,3)且与x轴的一个交点的坐标是(-5,0),求这个二次函数的解析式.
考点:待定系数法求二次函数解析式
专题:计算题
分析:根据二次函数顶点坐标设出顶点形式,把(-5,0)代入求出a的值,即可确定出解析式.
解答:解:设抛物线解析式为y=a(x+2)2+3,
把(-5,0)代入得:0=9a+3,即a=-
,
则抛物线解析式为y=-
(x+2)2+3=-
x2-
x+
.
把(-5,0)代入得:0=9a+3,即a=-
| 1 |
| 3 |
则抛物线解析式为y=-
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
点评:此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
如图,从边长为(a+4)的正方形纸片中剪去一个边长为(a+1)的正方形(a>0),剩余部分沿虚线又剪拼成一个长方形(不重叠、无缝隙),若拼成的长方形一边的长为3,则另一边的长为( )
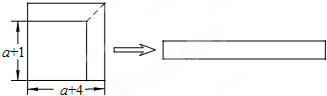

| A、2a+5 | B、2a+8 |
| C、2a+3 | D、2a+2 |
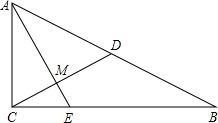 在Rt△ABC中,∠ACB=90°,D在AB中点,AE⊥CD于点M,
在Rt△ABC中,∠ACB=90°,D在AB中点,AE⊥CD于点M, CE是△ABC的外角∠ACD的平分线,AB的垂直平分线FG分别交AB,CE于F,G.联结GA,GB.求证:∠GAC=∠GBC.
CE是△ABC的外角∠ACD的平分线,AB的垂直平分线FG分别交AB,CE于F,G.联结GA,GB.求证:∠GAC=∠GBC.