题目内容
3.已知二次函数y=3(x-1)2-2的图象上有A(-$\sqrt{2}$,y1),B($\sqrt{2}$,y2),C(2,y3)三个点,则y1,y2,y3的大小关系是( )| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y1>y3>y2 | D. | y3>y2>y1 |
分析 根据二次函数的性质得抛物线的对称轴为直线x=1,由于抛物线开口向上,离对称轴越远的点所对应的函数值越大,于是比较点A、B、C到直线x=1的距离即可得到y1,y2,y3的大小关系.
解答 解:二次函数y=3(x-1)2-2的图象的对称轴为直线x=1,
而A(-$\sqrt{2}$,y1)到直线x=1最大,B($\sqrt{2}$,y2)到直线x=1的距离最小,抛物线开口向上,
所以y2<y3<y1.
故选C.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的性质.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
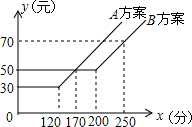 如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,下列四种结论:
如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,下列四种结论: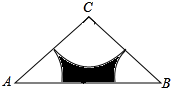 如图,在△ABC中,∠C=120°,CA=CB=6,分别以A,B,C为圆心,以3为半径画弧,三条弧与AB所围成的阴影部分的周长是3π+6$\sqrt{3}$-6.
如图,在△ABC中,∠C=120°,CA=CB=6,分别以A,B,C为圆心,以3为半径画弧,三条弧与AB所围成的阴影部分的周长是3π+6$\sqrt{3}$-6. 如图,AB∥CD,∠1=64°,FG平分∠EFC,则∠EGF=64°°.
如图,AB∥CD,∠1=64°,FG平分∠EFC,则∠EGF=64°°.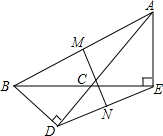 如图,BD,AE是钝角三角形ABC的两条高,M,N分别是AB,DE的中点,求证:MN⊥DE.
如图,BD,AE是钝角三角形ABC的两条高,M,N分别是AB,DE的中点,求证:MN⊥DE. 如图,BC是半⊙O的直径,点P是半圆弧的中点,点A是弧BP的中点,AD⊥BC于D,连结AB、PB、AC,BP分别与AD、AC相交于点E、F.
如图,BC是半⊙O的直径,点P是半圆弧的中点,点A是弧BP的中点,AD⊥BC于D,连结AB、PB、AC,BP分别与AD、AC相交于点E、F.