题目内容
14．
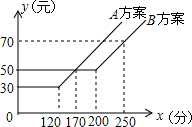如图，某电信公司提供了A，B两种方案的移动通讯费用y（元）与通话时间x（分）之间的关系，下列四种结论：①若通话时间少于120分，则A方案比B方案便宜20元；
②若通话时间超过200分，则B方案比A方案便宜12元；
③若通讯费用为0元，则B案比A方案的通话时间多；
④若两种方案通讯费用相差10元，则通话时间是145分或185分．
其中正确的结论是①②③．
分析 当B方案为50元时，A方案如果是40元或者60元，才能使两种方案通讯费用相差10元，先求两种方案的函数解析式，再求对应的时间．
解答 解：A方案的函数解析式为：yA=$\left\{\begin{array}{l}{30（0＜x≤120）}\\{\frac{2}{5}x-18（x＞120）}\end{array}\right.$；
B方案的函数解析式为：yB=$\left\{\begin{array}{l}{50（0＜x≤200）}\\{\frac{2}{5}x-30（x＞200）}\end{array}\right.$；
当B方案为50元，A方案是40元或者60元时，两种方案通讯费用相差10元，
将yA=40或60代入，得x=145分或195分，故D错误；
观察函数图象可知①②③正确．
故答案是：①②③．
点评 本题考查了分段函数的应用，需注意两种付费方式都是分段函数，难点是根据所给函数上的点得到两个函数的解析式，而后结合图象进行判断．
练习册系列答案
相关题目
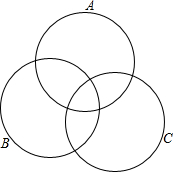已知A、B、C三个数集，每一个数集中所包含的数都写在各自的大括号内，请把这些数填在图圈内相应的位置．
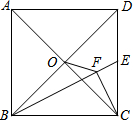如图，正方形ABCD的面积为20，对角线AC、BD相交于点O，点E是边CD的中点，过点C作CF⊥BE于F，连接OF，则OF的长为$\sqrt{2}$．
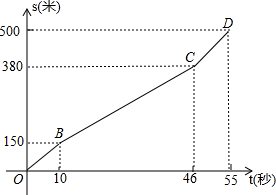为迎接2015短道速滑世界杯，中国短道速滑队进行多种强度的训练．在一次500m训练中，周洋所滑的路程s米与所用时间t秒之间的函数图象为折线OBCD．和她同时起滑的李坚柔前300m的速度保持在10m/s，后来速度改慢，但还保持匀速滑行，结果和周洋同时到达终点．
3．已知二次函数y=3（x-1）2-2的图象上有A（-$\sqrt{2}$，y1），B（$\sqrt{2}$，y2），C（2，y3）三个点，则y1，y2，y3的大小关系是（ ）
| A． | y1＞y2＞y3 | B． | y2＞y1＞y3 | C． | y1＞y3＞y2 | D． | y3＞y2＞y1 |