题目内容
15．
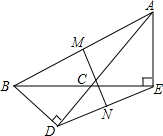如图，BD，AE是钝角三角形ABC的两条高，M，N分别是AB，DE的中点，求证：MN⊥DE．
分析 连接EM、MD，首先根据直角三角形的性质可得MD=ME，再根据等腰三角形三线合一的性质可得MN⊥DE．
解答 
证明：连接EM、MD，
∵BD，AE是钝角三角形ABC的两条高，
∴∠BEA=90°，∠BDA=90°，
∵M，N分别是AB，DE的中点，
∴DM=EM=$\frac{1}{2}$AB，
∴△DME是等腰三角形，
∵N是DE中点，
∴MN⊥DE．
点评 此题主要考查了等腰三角形的性质，以及直角三角形的性质，关键是掌握在直角三角形中，斜边上的中线等于斜边的一半．
练习册系列答案
口算题天天练系列答案
相关题目
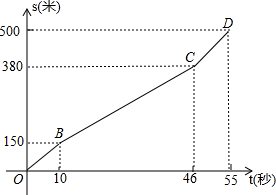为迎接2015短道速滑世界杯，中国短道速滑队进行多种强度的训练．在一次500m训练中，周洋所滑的路程s米与所用时间t秒之间的函数图象为折线OBCD．和她同时起滑的李坚柔前300m的速度保持在10m/s，后来速度改慢，但还保持匀速滑行，结果和周洋同时到达终点．
3．已知二次函数y=3（x-1）2-2的图象上有A（-$\sqrt{2}$，y1），B（$\sqrt{2}$，y2），C（2，y3）三个点，则y1，y2，y3的大小关系是（ ）
| A． | y1＞y2＞y3 | B． | y2＞y1＞y3 | C． | y1＞y3＞y2 | D． | y3＞y2＞y1 |
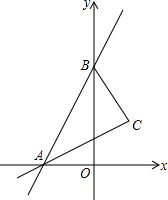如图，直线y=7x+7交x轴于点A，交y轴于点B．