题目内容
1.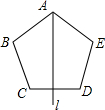 如图所示,在正五边形的对称轴直线l上找点P,使得△PCD、△PDE均为等腰三角形,则满足条件的点P有( )
如图所示,在正五边形的对称轴直线l上找点P,使得△PCD、△PDE均为等腰三角形,则满足条件的点P有( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
分析 根据轴对称的性质得到△PCD是等腰三角形,欲使△PDE为等腰三角形,则点P是线段DE的角平分线与l的交点.
解答 解:∵P点在直线L上,
∴此时PC=PD,
即△PCD是等腰三角形,
分为三种情况:①作DE的垂直平分线,交直线l于一点P,此时PE=PD;
②以D为圆心,以DE为半径,交直线l于两点,此时DP=DE;
③以E为圆心,以DE为半径,交直线l于两点,此时EP=DE;
共1+2+2=5点.
故选B.
点评 本题考查了等腰三角形的判定,轴对称性质的应用,能求出符合的所有情况是解此题的关键.

练习册系列答案
相关题目
19.已知∠α与∠β互余,∠β和∠γ互补,则∠γ的度数为( )
| A. | α | B. | β | C. | 90°+α | D. | 90°+β |
10.下列方程中,解为x=1的是( )
| A. | x-2=-1 | B. | 2x+3=1 | C. | 1=1+x | D. | 2x-3=1 |
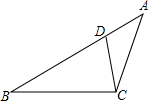 已知:如图,在△ABC中,D是AB上一点,且∠ACD=∠B,若AC=5,AB=9,CB=6.
已知:如图,在△ABC中,D是AB上一点,且∠ACD=∠B,若AC=5,AB=9,CB=6.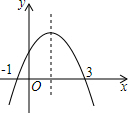 如图为二次函数y=ax2+bx+c(a≠0)的图象,对称轴是x=1,则下列说法:①b>0;②2a+b=0;③4a-2b+c>0;④3a+c>0;⑤m(ma+b)<a+b(常数m≠1).其中正确的个数为( )
如图为二次函数y=ax2+bx+c(a≠0)的图象,对称轴是x=1,则下列说法:①b>0;②2a+b=0;③4a-2b+c>0;④3a+c>0;⑤m(ma+b)<a+b(常数m≠1).其中正确的个数为( )