题目内容
6．化简：（x-$\frac{x-4}{x-3}$）÷$\frac{{x}^{2}-4}{x-3}$=$\frac{x-2}{x+2}$．分析 首先把括号内的式子通分相减，然后把除法转化为乘法，计算乘法即可求解．
解答 解：原式=$\frac{x（x-3）-（x-4）}{x-3}$•$\frac{x-3}{（x+2）（x-2）}$
=$\frac{{x}^{2}-4x+4}{x-3}$•$\frac{x-3}{（x+2）（x-2）}$
=$\frac{（x-2）^{2}}{x-3}$•$\frac{x-3}{（x+2）（x-2）}$
=$\frac{x-2}{x+2}$．
故答案是：$\frac{x-2}{x+2}$．
点评 本题考查了分式的化简，通分、因式分解和约分是解答的关键．
练习册系列答案
相关题目
1．
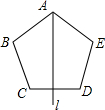如图所示，在正五边形的对称轴直线l上找点P，使得△PCD、△PDE均为等腰三角形，则满足条件的点P有（ ）
如图所示，在正五边形的对称轴直线l上找点P，使得△PCD、△PDE均为等腰三角形，则满足条件的点P有（ ）| A． | 4个 | B． | 5个 | C． | 6个 | D． | 7个 |
如图，在梯形ABCD中，AD∥BC，EF∥BC，EF分别交AB，CD，AC于点E、F、G．若$\frac{CF}{FD}$=$\frac{2}{3}$，则$\frac{BE}{EA}$=$\frac{2}{3}$，$\frac{CG}{CA}$=$\frac{2}{5}$，$\frac{AG}{AC}$=$\frac{3}{5}$，$\frac{AB}{EB}$=$\frac{5}{2}$．
如图，矩形ABCD∽矩形ECDF，且AB=BE，求BC与AB的比值．